1.
p=34cm
a=x
b=x-3
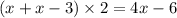
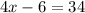

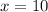
Длина 10, Ширина 10-3=7
2)
Известно, что туристическую группу из 38 человек расселили в двухместные и трёхместные номера.
При этом всего было занято 14 номеров.
Требуется вычислить сколько среди них было двухместных и сколько трёхместных.
Обозначим количество двухместных номеров "х", а количество трёхместных "у".
Тогда:
х + у = 14
х = 14 - у.
Составим уравнение.
2х + 3у = 38,
Подставим значение "х".
2 * (14 - у) + 3у = 38,
28 - 2у + 3у = 38,
у = 38 - 28 = 10 трёхместных номеров.
14 - 10 = 4 двухместных номеров.
наим. -4750
наиб. 34
Объяснение:
f(x) = x⁵+15x³-50x
x ∈ [-5 ; 0]
экстремумы (мин или макс) в точках f'(x) = 0
f'(x) = 5x⁴ + 45x³ - 50
5x⁴ + 45x³ - 50 = 0
x⁴ + 9x² - 10 =0
x² = y ≥ 0
y² + 9y -10 =0
D = 121
y = (-9 +11)/2 = 1, второй корень отрицательный - не подходит
x² = 1
x = -1, т. к. 1 ∉ [-5 ; 0]
f(-1) = -1 -15 + 50 = 34
узнать мин или макс можно или через 2-ю производную или сравнить со значениями в окрестности.
Сравним:
f(0) = 0 < 34
f(-2) = -32 - 120 + 100 = -52 < 34
Значит наибольшее на отрезке = 34 и это единственный экстремум на промежутке, значит наименьшее будет на его краях, при 0 уже нашли найдем при -5
(-5)⁵ + 15*(-5)³ + 250 = -3125 - 1875 + 250 = -4750 это и будет наименьшим значением
Формула очень простая:
N = N0*(1 + p/100)^n
Здесь N0 = 8000 - начальный вклад, N - результат.
p - проценты, n - годы.
N = 8000*(1,09)^4 = 8000*1,41158 = 11292,65 рублей