Вероятность того, что у Незнайки будет большее количество очков, равна вероятности благоприятствующих исходов (то есть, исходов, в которых действительно у Незнайки больше очков) ко всем [элементарным] исходам.
На таблице ниже (первое число означает количество очков Незнайки, а второе - количество очков Кнопочки) видно, что число благоприятствующих исходов (выделены красным) равно 15, а число всех исходов - 6² = 36.
Значит, у них сейчас разница в 12 монет (у Васи на 12 монет больше, чем у Пети). Если же ещё и Петя даст 9 монет, то эта разница увеличится на 9+9 = 18 монет. Итого она будет составлять 12+18 = 30 монет. Получается, что у Васи может в таком случае быть больше на 30 монет.
Если у одного минимальное количество монет (1 монета), то коэффициент K будет наибольший. А если у одного из них 1 монета, а у второго на 30 монет больше, то получается, что у второго — 31 монета. 31/1 = в 31 раз.
На таблице ниже (первое число означает количество очков Незнайки, а второе - количество очков Кнопочки) видно, что число благоприятствующих исходов (выделены красным) равно 15, а число всех исходов - 6² = 36.
⇒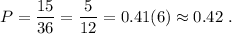
Задача решена!
ответ: 0.42 .