Вариант 1 найдите неизвестный член пропорции а) 15: 10=х: 40 б) 3,6: 4,2=6: х в) 3: х=3\8: 1\4 г) х: 1 1\3=6: 4 д) х: 3,86=2,5: 2 1\2 вариант2 найдите неизвестный член пропорции а) 20: х=4: 6 б) х: 4,5=0,4: 0,5 в) 5\8: 1\6=х: 4 г) 1 1/3: 4=4: х д) 5,84: х=3 1\4: 3,25

👇

Ответ:

Мур6954

22.05.2022

ВАРИАНТ 1.
а) 15/10 = x/40
x = (15*40)/10
x = 60
б) 3,6/4,2 = 6/x
x = (4,2*6)/3,6
x = 7
в) 3/x = 3/8:1/4
3/x = 3/2
x = 2
г) x:11/3 = 6/4
3x/11 = 6/4
3x = (11*6)/4
3x = 16,5 |:3
x = 5,5
д) x/3,86 = 2,5:2 1\2
x/3,84 = 1
x = 3,84
ВАРИАНТ 2.
а) 20/x = 4/6
x = (20*6)/4
x = 30
б) x/4,5 = 0,4/0,5
x = (4,5*0,4)/0,5
x = 3,6
в) 5/8 : 1/6 = x/4
15/4 = x/4
x = 15
г) 1 1\3:4 = 4/x
1/3 = 4/x
x = 4*3
x = 12
д) 5.84/x = 3 1\4 :3.25
5.84/x = 3,25/3,25
5.84/x = 1
x = 5.84

4,8(37 оценок)

Открыть все ответы

Ответ:

aazzziizz

22.05.2022

5 arccos 1\2 + 3 arcsin (-корень из 2\2)
Оба значения табличные для cos и sin
$5 arccos \frac{1}{2} + 3 arcsin (- \frac{ \sqrt{2} }{2}) = \\ 5 * \frac{ \pi }{3} +3*(- \frac{ \pi }{4} ) = \\ \frac{5 \pi }{3} - \frac{3 \pi }{4} = \frac{11 \pi }{12}$

sin ( 4 arccos ( - 1\2) - 2 arcctg корень из 3\3)
Оба значения табличные для cos и ctg
$sin [ 4 arccos ( - \frac{1}{2}) - 2 arcctg \frac{ \sqrt{3} }{3} ] = \\ sin [4* \frac{2 \pi }{3} - 2* \frac{ \pi }{3} ] = \\ sin[ \frac{8 \pi }{3} - \frac{2 \pi }{3} ] = sin(2 \pi ) = 0$

6 sin^2x + 5cosx-7=0
Сначала использовать основное тригонометрическое тождество
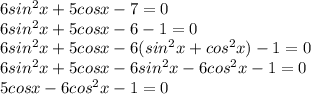
$6 sin^2x + 5cosx-7=0 \\ 6 sin^2x + 5cosx-6 - 1 =0 \\ 6 sin^2x + 5cosx-6( sin^{2}x + cos^{2}x) - 1 =0 \\ 6 sin^2x + 5cosx-6 sin^{2}x - 6cos^{2}x - 1 =0 \\ 5cosx - 6cos^{2}x - 1 =0$
Это обыкновенное квадратное уравнение, в котором переменной является cos x
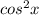$- 6cos^{2}x +5cosx - 1 =0 \\ D = 25 - 4*(-6)*(-1) = 25 - 24 = 1 \\ cos x_{1} = \frac{-5-1}{-12} = \frac{1}{2} \\ cos x_{2} = \frac{-5+1}{-12} = \frac{1}{3} \\ x_{1} = \frac{+}{} \frac{ \pi }{3} + 2 \pi n \\ x_{2} = \frac{+}{} arccos \frac{1}{3} +2 \pi m$ , n,m∈Z

2sin^2x + sinx cosx - 3 cos^2x=0
Проверить, что $cos^{2} x$ не является корнем ( на ноль делить нельзя), а потом все уравнение почленно разделить на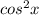 $cos^{2} x$
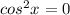
$cos^{2} x = 0$
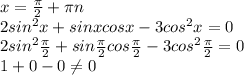
$x = \frac{ \pi }{2} + \pi n \\ 2sin^2x + sinx cosx - 3 cos^2x=0 \\ 2sin^2 \frac{ \pi }{2} + sin \frac{ \pi }{2} cos \frac{ \pi }{2} - 3 cos^2 \frac{ \pi }{2}=0 \\ 1+0-0 \neq 0$
Не корень, можно делить
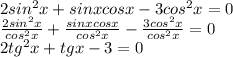
$2sin^2x + sinx cosx - 3 cos^2x=0 \\ \frac{2 sin^{2}x }{ cos^{2} x} + \frac{sinx cosx}{cos^{2} x} - \frac{3cos^{2} x}{cos^{2} x} =0 \\ 2 tg^{2}x +tgx-3 = 0$
Обыкновенное квадратное уравнение с переменной tg x
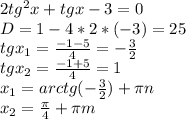
$2 tg^{2}x +tgx-3 = 0 \\ D = 1 - 4*2*(-3) = 25 \\ tg x_{1} = \frac{-1-5}{4} = -\frac{3}{2} \\ tg x_{2} = \frac{-1+5}{4} = 1 \\ x_{1} =arctg( -\frac{3}{2} ) + \pi n \\ x_{2} =\frac{ \pi }{4} + \pi m$
n,m ∈ Z

4,8(38 оценок)

Ответ:

Гипопофото

22.05.2022

1)
а) Д= 25+96=121
x1= (-5+11)/2=3
х2= (-5-11)/2=-13

б) Д= 361+168=529
х1= (19+23)/6=7
х2=(19-23)/6= 4/6

2)a) x^2 -14x +49 = (x-7)^2
б) x^2 + 5x -6 = (x+5)^2 -5x -31
в)

3)x^2 -4x +31>0
Д=16-4*31 < 0 => нету пересечения с осью ox, т.к. ветви вверх, то всегда >0
б) 9x^2 +24x +16
Д= 576-576=0 => 1 т. пересечения с осью ox, ветви вверх => >=0

5) 4x^2 -x = x(4x-1)
б) x^2 +7x+10
Д=49-40=9
x1= -7+3/8= -1/2
x2= -5/4
x^2+7x+10=(x+1/2)(x+5/4)
В) 5x^2 - 7x +2
Д= 49-40=9
x1 = 7+3/10=1
x2= 7-3/10= 4/10=0,4
5x^2 - 7x +2 = 5(x-1)(x-0,4) про 5 не уверен
Г) -2x^2-9x-9=2x^2 + 9x +9
Д=81-72=9
x1= -9-3/4=-3
x2=-9+3/4= -6/4
2x^2 + 9x + 9 = 2(x+3)(x+6/4) про 2 не уверен :C