пример.рассмотрим следующую линейную функцию: y = 5x – 3.
1) d(y) = r;
2) e(y) = r;
3) функция общего вида;
4) непериодическая;
5) точки пересечения с осями координат:
ox: 5x – 3 = 0, x = 3/5, следовательно (3/5; 0) – точка пересечения с осью абсцисс.
oy: y = -3, следовательно (0; -3) – точка пересечения с осью ординат;
6) y = 5x – 3 – положительна при x из (3/5; +∞),
y = 5x – 3 – отрицательна при x из (-∞; 3/5);
7) y = 5x – 3 возрастает на всей области определения; линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел. здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.
в частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси ox, проходящая через точку с координатами (0; b).
если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью.
смысл коэффициента b – длина отрезка, который отсекает прямая по оси oy, считая от начала координат.
смысл коэффициента k – угол наклона прямой к положительному направлению оси ox, считается против часовой стрелки.
свойства линейной функции:
1) область определения линейной функции есть вся вещественная ось;
2) если k ≠ 0, то область значений линейной функции есть вся вещественная ось. если k = 0, то область значений линейной функции состоит из числа b;
3) четность и нечетность линейной функции зависят от значений коэффициентов k и b.
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) свойством периодичности линейная функция не обладает;
5) точки пересечения с осями координат:
ox: y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс.
oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.
замечание.если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.
6) промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞),
y = kx + b – отрицательна при x из (-∞; -b/k).
b) k < 0; kx + b < 0, kx < -b, x < -b/k.
y = kx + b – положительна при x из (-∞; -b/k),
y = kx + b – отрицательна при x из (-b/k; +∞).
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b < 0; y = kx + b отрицательна на всей области определения.
7) промежутки монотонности линейной функции зависят от коэффициента k.
k > 0, следовательно y = kx + b возрастает на всей области определения,
k < 0, следовательно y = kx + b убывает на всей области определения.
8) графиком линейной функции является прямая. для построения прямой достаточно знать две точки. положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Площадь фигуры ограниченной линиями f(x)=x+5, g(x)=6/x, x=-2, x=6 и осью 0x равна (16,5 +6 ln6) ед.²
Объяснение:
Требуется найти площадь фигуры ограниченной линиями f(x)=x+5, g(x)=6/x, x=-2, x=6 и осью 0x.
Площадь фигуры найдем по формуле:
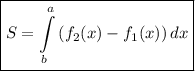
Дано:
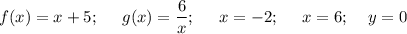
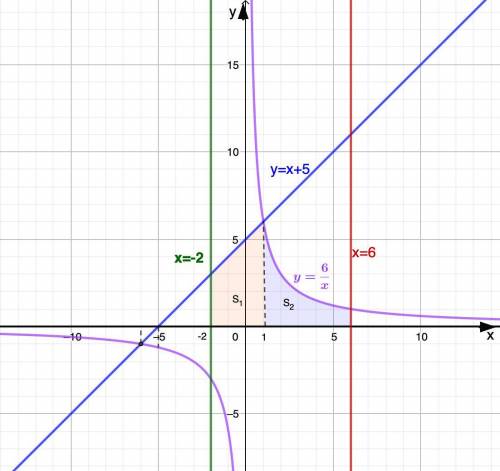
Построим графики и определим область, которая ограничена данными линиями.
1. 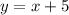
-линейная функция, график прямая.
Для построения достаточно две точки:
х = -5, у=0;
х = 1, у=6.
Строим график.
2. 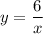
-функция обратной пропорциональности, график гипербола, расположенная в первой и третьей четвертях.
Возьмем четыре точки:
х = 1, у = 6;
х = 2, у = 3;
х = 3, у = 2;
х = 6, у = 3.
Строим одну ветвь гиперболы. Вторую строим симметрично начала координат.
3. Точки пересечения данных графиков:
(1; 6) и (-6; -1).
4. Видим, что искомая площадь состоит из двух площадей:
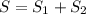
5. Найдем S₁.
Линия сверху f₂(x) = x+5, снизу f₁(x) = 0, слева b = -2, справа a = 1.
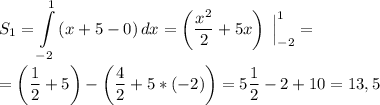
6. Найдем S₂.
f₂(x) = 6/x, f₁(x) = 0, b = 1, a = 6.
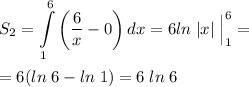
7. S = S₁ +S₂ = 13,5 + 6 ln6 (ед²)
————-
X^2
X^20
——-
X^2
X^18
Вот и все