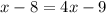
Объяснение:
Объяснение:
Постройте график функции y=3x+2
Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно: 0; 1; -1.
2) значение аргумента, при котором значение функции равно 0.
3) несколько значений аргумента, при которых функция принимает положительные значения.
4)несколько значений аргумента, при которых функция принимает отрицательные значения.
y=3x+2
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у -1 2 5
1)Согласно графика при х=0 у=2
при х= 1 у= 5
при х= -1 у= -1
2)Согласно графика у=0 при х= -2/3 (≈ -0,67)
3)Согласно графика у>0 при х∈( - 2/3; ∞), положительные значения у принимает при х от -2/3 до + бесконечности, например, 1, 5,10.
4)Согласно графика у<0 при х∈(- ∞; -2/3), отрицательные значения у принимает при х от -2/3 до - бесконечности, например, -2, -7, -25.
-7,5(х - 10)(х + 39) = 0
(-7,5х + 75)(х + 39) = 0
Чтобы произведение равнялось 0, достаточно, чтобы один из множителей был равен 0.
-7,5х + 75 = 0 х + 39 = 0
-7,5х = -75 х = -39
х = -75 : (-7,5)
х = 10
(-7,5х + 75)(х + 39) = 0
-7,5х² + 75х - 292,5х + 2925 = 0
-7,5х² - 217,5х + 2925 = 0
Разделим обе части уравнения на (-7,5)
х² + 29х - 390 = 0
D = b² - 4ac = 29² - 4 · 1 · (-390) = 841 + 1560 = 2401
√D = √2401 = 49
х₁ = (-29-49)/(2·1) = (-78)/2 = -39
х₂ = (-29+49)/(2·1) = 20/2 = 10
ответ: х₁ = -39; х₂ = 10.
2x = 4 0x = 0 0x = 7
x = 2 x ∈(-∞;+∞) решений нет
2a) 5 - 2x = 0 б) x - 8 = 4x - 9 x - 8 = - 4x - 9
- 2x = - 5 x - 4x = - 9 + 8 x + 4x = 8 - 9
x = 2,5 - 3x = - 1 5x = - 1
x = 1/3 x = - 0,2