См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒ м
м
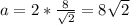 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
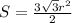 ⇒
⇒
 см
см
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
 ≈151 см²
≈151 см²
(где n - градусная мера дуги сектора)

Площадь - это число, показывающие сколько места занимает фигура. Площадь вычисляется с произведения. Для того, чтобы найти площадь, нужно ширину умножить на длину. У квадрата все стороны равны, а значит ширина равна длине. Имея эти данные, мы можем вычислить его стороны. В условии сказано, что одна из сторон равна 4 м., а стало быть и остальные равны 4 м. Теперь мы можем вычислить площадь квадрата(учитывая то, что ширина равна длине). Обозначается площадь латинской буквой S:
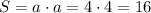
Но это ещё не всё. Площадь измеряется в квадратах. К примеру: см², мм², м², и т.д.
Так как в условии даны м., значит и площадь будет м².
ответ: 16 м²

Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
Задание № 3:
Сколько корней имеет уравнение: |x|=|x−1|+x−3?
Условию раскрытия модуля соответствует только третья строчка.
ОТВЕТ: 1