y = x³ - 4x²
Найдём производную :
y' = (x³)' - 4(x²)' = 3x² - 8x
Найдём критические точки, для этого приравняем производную к нулю.
y' = 0
3x² - 8x = 0
x(3x - 8) = 0
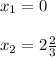
Отметим критические точки на числовой прямой и выясним знаки производной на промежутках, на которые эти точки разбивают числовую прямую .
y'(x) + - +
____________0___________2 2/3_____________
y(x) ↑ ↓ ↑
На промежутках (- ∞ ; 0] и [2 2/3 ; + ∞) -функция возрастает
На промежутке [0 ; 2 2/3] - функция уюывает
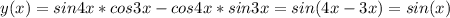
есть 
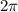
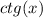равен 
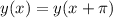
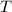- искомый период, тогда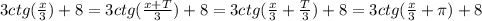
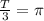
относительно оси OX на 8 единиц вверх, также не влияя на период
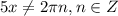
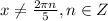
- это симметричное относительно начала координат множество точек,
также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
запутался в числах
соре