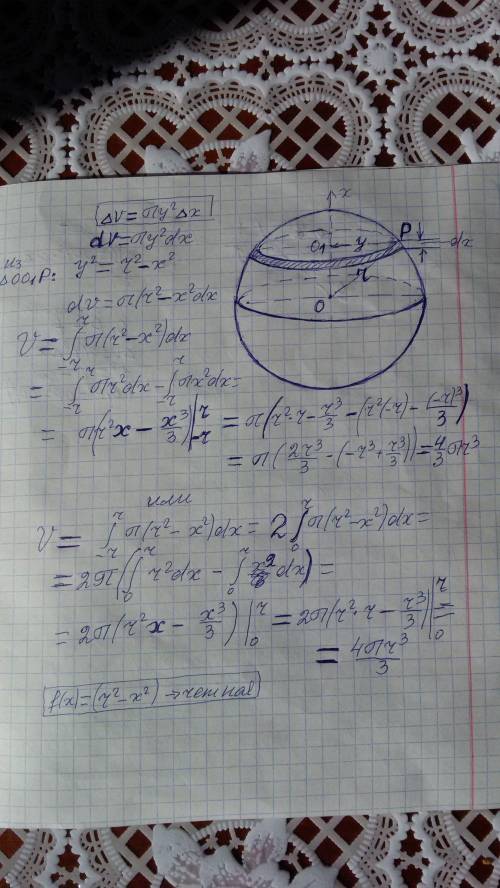99 , 11 клас, разобраться в этом бреде! объем шара, как известно, (4/3)*pi*(r^3). объем куба (2*r)^3 = 8*(r^3). а объем чего же тогда получаю я, когда решаю определенный интеграл: объем той фигуры, которая получится, если вынуть сферу из куба? но ее объем должен быть приблизительно в 2 раза объем фигуры, которая получится, если разрезать сферу по оси y и соединить противоположными концами? но ее объем равен объему сферы, он тоже в 2 раза больше. я знаю, что объем шара выводится так: но я не могу понять, в чем разница: брать r^2-x^2 или просто x^2, мне кажется, объемы в этом случае должны быть равными, а они отличаются в 2 раза. , объясните мне, чего я не