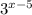Question

Надо решить показательное уравнение: 3ˣ⁻⁵ + 4ˣ⁻⁵ = 91

Answer 1

Теорема. 1) Если на некотором промежутке функция f(x) возрастает (или убывает), то  уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).

$3^{x-5}+4^{x-5}$ - возрастающая, как сумма возрастающих функций.

f(x) = 91

Эти две графики пересекаются в одной точке, то есть, по теореме выше сказанному, уравнение имеет единственное решение и его найти можно путем подбора.

ответ: х=8.

Answer 2

Я рассуждал так.
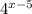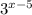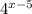Изначально можно установить что х>5, т.к. при х<5 значение $3^{x-5}$ и $4^{x-5}$ стремятся к нулю, а значит равенство не будет выполняться. Так же значение $3^{x-5}$ или $4^{x-5}$ не могут быть по отдельности равны 91 (максимальным целым показателем степени для 3 является 4, для 4 является 3). То есть показатель степени находится в пределах   5<x<9. Перебрав оставшиеся целые числа 6,7,8 выбираем 8 (т.к. равенство выполняется).
P.S. Очевидно, что показателем степени будет целое число.