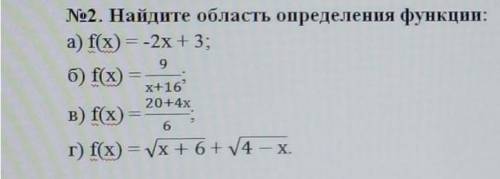
а) все числа
б) х+16 ≠0
х≠-16
хЄ(- бесконечность; -16) объедение (-16; +бесконечности)
в) все числа
г) х+6≥0 и 4 - х ≥0
х≥-6 х≤4
хЄ[-6;4]
Решить систему линейных уравнений методом подстановки и методом сложения:
{
y
+
2
x
=
1
y
−
x
=
3
Решение методом подстановки.
{
y
+
2
x
=
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
(
−
2
x
+
1
)
−
x
=
3
⇒
{
y
=
−
2
x
+
1
−
3
x
−
2
=
0
⇒
{
y
=
−
2
x
+
1
x
=
−
2
3
⇒
{
y
=
7
3
x
=
−
2
3
y
=
2
1
3
;
x
=
−
2
3
Решение методом сложения.
{
y
+
2
x
=
1
y
−
x
=
3
Вычитаем уравнения:
−
{
y
+
2
x
=
1
y
−
x
=
3
(
y
+
2
x
)
−
(
y
−
x
)
=
1
−
3
3
x
=
−
2
x
=
−
2
3
Подставиим найденную переменную в первое уравнение:
(
−
2
3
)
+
2
x
=
1
y
=
7
3
y
=
2
1
3
;
x
=
−
2
3
Объяснение:
Объяснение:
а) любое число, x принадлежит множеству R
б) любое число кроме -16
То есть
(-бесконечность;-16)v(-16;+бесконечность)
в) любое число, x принадлежит множеству R
г) подкоренное выражение должно быть больше, либо равнятся нулю.
x>=-6 ; x<=4, то есть [-6;4]