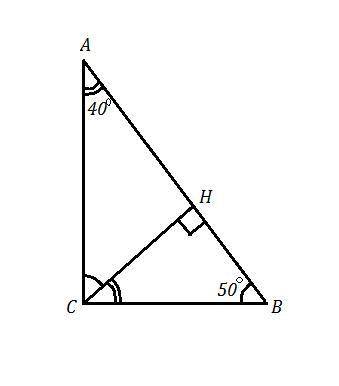
ΔАВС , ∠С=90° , ∠В=50° ⇒ ∠А=90°-∠В=90°-50°=40°
СН ⊥ АВ ⇒ ∠СНА=90° и ∠СРВ=90° .
Рассм. ΔВСН . Он прямоугольный и ∠В=50° , тогда ∠ВСН=90°-50°=40°. Это угол, образованный высотой СН с меньшим катетом (катет ВС лежит против меньшего острого угла ΔАВС).
Рассм. ΔАСН . Он прямоугольный и ∠А=40° , тогда ∠АСН=90°-40°=50°. Это угол, образованный высотой СН с бОльшим катетом АС (катет АС лежит против бОльшего острого угла ΔАВС).
Замечание. Так как у треугольников ΔАВС , ΔВСН и ΔАСН все три угла равны, то эти треугольники подобны .
Дано неравенство ((2x-3) / (x^2+2x)) > 0,125 или ((2x-3) / (x^2+2x)) > 1/8.
Умножим обе части на 8: (16x - 24) / (x^2+2x) > 1.
По свойству дроби числитель больше знаменателя:
(16x - 24) > (x^2+2x). Перенесём левую часть вправо.
Получим равносильное неравенство x^2 + 2x - 16х + 24 < 0 или
x^2 - 14х + 24 < 0. Д = 196 - 4*24 = 100.
х1 = (14 + 10)/2 = 12, х2 = (14 - 10)/2 = 2.
Исходное неравенство можно представить так:
(х - 12)(х - 2)/(х(х + 2)) < 0.
Используем метод интервалов: -2 0 2 12
+ - + - +
Отсюда ответ: -2 < x < 0; 2 < x < 12.
Корень (1,0)
Область определение :xєR
Минимум :(3, - 4)
Пересечение с осью y:(0, 5)