Question

Выполните действия 1) 11+√21 / 11-√21 + 11-√21 / 11+√21 2) 1 / 11-2√30 - 1 / 11+2√30 3) 5 / 3+2√2 + 5 / 3-2 √2

Answer 1

.............................................

Answer 2

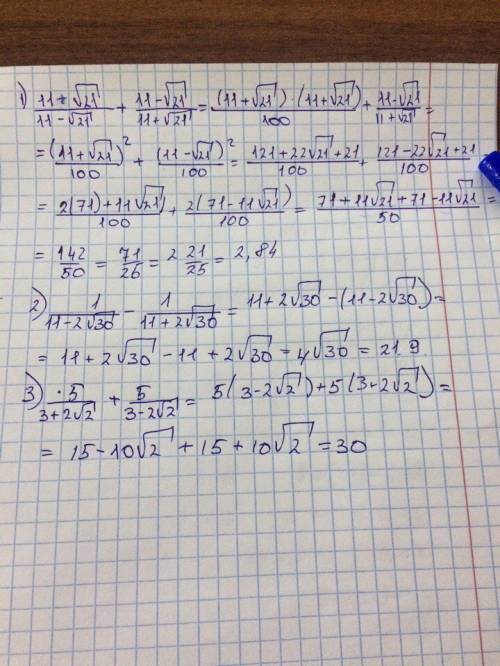
Приводим к общему знаменателю и применим следующие формулы сокращённого умножения:

а) (a+b)·(a+b)=a²+2·a·b+b²;

б) (a-b)·(a-b)=a²-2·a·b+b²;

в) (a+b)·(a-b)=a²-b².

$\tt \displaystyle 1) \;\; \frac{11+\sqrt{21} }{11-\sqrt{21} }+ \frac{11-\sqrt{21} }{11+\sqrt{21} } = \frac{(11+\sqrt{21} ) \cdot (11+\sqrt{21} )+(11-\sqrt{21} ) \cdot (11-\sqrt{21} )}{(11-\sqrt{21}) \cdot (11+\sqrt{21} )}= \\\\=\frac{121+2 \cdot 11 \cdot \sqrt{21} +21+121-2 \cdot 11 \cdot \sqrt{21} +21}{121-21}=\frac{284}{100}=2,84;$

$\tt \displaystyle 2) \;\; \frac{1}{11-2 \cdot \sqrt{30} }- \frac{1}{11+2 \cdot \sqrt{30} } = \frac{1 \cdot (11+2 \cdot \sqrt{30} )-1 \cdot (11-2 \cdot \sqrt{30} )}{(11-2 \cdot \sqrt{30} ) \cdot (11+2 \cdot \sqrt{30} )}= \\\\=\frac{11+2 \cdot \sqrt{30} -11+2 \cdot \sqrt{30} }{121-4 \cdot 30}=\frac{4 \cdot \sqrt{30} }{121-120}=4 \cdot \sqrt{30};$

$\tt \displaystyle 3) \;\; \frac{5}{3+2 \cdot \sqrt{2} }+\frac{5}{3-2 \cdot \sqrt{2} } = \frac{5 \cdot (3-2 \cdot \sqrt{2} )+5 \cdot (3+2 \cdot \sqrt{2} )}{(3+2 \cdot \sqrt{2} ) \cdot (3-2 \cdot \sqrt{2})}= \\\\=\frac{15-10 \cdot \sqrt{2} +15+10 \cdot \sqrt{2} }{9-4 \cdot 2}=\frac{30}{9-8}=30.$

Answer 3

$1)~2.84; ~2)~ 4\sqrt{30};~3)~30$

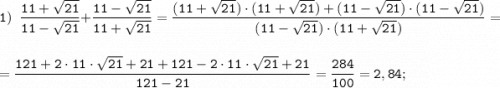
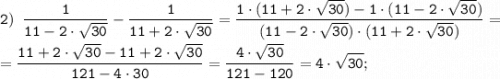
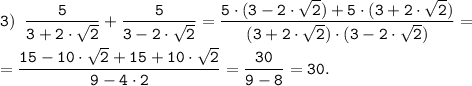
Объяснение:

$\displaystyle1)~\frac{11+\sqrt{21}}{11-\sqrt{21}}^{\backslash 11 + \sqrt{21}} + \frac{11-\sqrt{21} }{11 + \sqrt{21}}^{\backslash 11 - \sqrt{21}} = \frac{(11+\sqrt{21})^2+(11-\sqrt{21})^2}{(11+\sqrt{21})(11-\sqrt{21})} = \\[1.5em] = \frac{11^2+2\cdot 11\cdot\sqrt{21}+(\sqrt{21})^2+11^2-2\cdot 11 \cdot \sqrt{21} + (\sqrt{21})^2}{11^2 - (\sqrt{21})^2} = \\[1.5em] \\ = \frac{121+21+121+21}{121-21} = \frac{284}{100} = 2.84$

$\displaystyle 2)~\frac{1}{11-2\sqrt{30}}^{\backslash 11 + 2\sqrt{30}} - \frac{1}{11+2\sqrt{30}}^{\backslash11-2\sqrt{30}} = \frac{11+2\sqrt{30}-11+2\sqrt{30}}{(11+2\sqrt{30})(11-2\sqrt{30})} = \\[1.5em] = \frac{4\sqrt{30}}{11^2-(2\sqrt{30})^2} = \frac{4\sqrt{30}}{121-120} = 4\sqrt{30}$

$\displaystyle 3) ~ \frac 5 {3+2\sqrt 2} + \frac 5 {3 - 2\sqrt 2} = 5\cdot\left (\frac 1 {3+2\sqrt 2}^{\backslash3-2\sqrt 2} + \frac 1 {3 - 2\sqrt 2}^{\backslash 3+2\sqrt 2}\right ) = \\[1.5em] = 5\cdot \frac {3-2\sqrt 2 + 3+2\sqrt 2}{(3+2\sqrt 2)(3-2\sqrt 2)} = 5 \cdot \frac{6}{3^2-(2\sqrt 2)^2}= 5 \cdot \frac{6}{9-8} = 5\cdot 6= 30$