35 км/ч
Объяснение:
Дано:
S₁ = 35 км
S₂ = 34 км
t = 2 ч
Vр = 1 км/ч
V - ?
1)
Заметим, что собственная скорость лодки равна скорости ее движения по озеру:
V₁ = V
Время, затраченное на движение по озеру:
t₁ = S₁ / V₁
или
t₁ = S₁ / V.
2)
Время, затраченное на движение по реке.
Заметим, что река впадает в озеро, а это значит, что лодка двигалась против течения: V₂ = V - Vp
t₂ = S₂ / V₂ или
t₂ = S₂ / (V - Vp)
3)
Общее время движения:
t = t₁ + t₂
или
t = S₁ / V₁ + S₂ / (V - Vp)
Подставляем данные и решаем уравнение:
2 = 35 / V + 34 / (V - 1)
2·V·(V-1) = 35·(V-1) + 34·V
2·V² - 2·V = 35·V - 35 +34·V
2·V² - 71·V + 35 = 0
Решая это квадратное уравнение, получаем:
V = (71-69)/4 = 0,5 км/ч (слишком маленькая скорость...)
V = (71+69)/4 = 35 км/ч
Объяснение:
у = х⁴ + 4х³
1. ОДЗ: х∈R
2.Четность, нечетность.
у(-х) = (-х)⁴ + 4(-х)³=х⁴-4х³
у(-х) ≠ у(х) ≠ -у(х) ⇒ функция не является четной или нечетной, то есть - общего вида.
3. Пересечение с осями.
х=0 ⇒ у=0
у=0 ⇒ х⁴ + 4х³ = 0; х³(х + 4) = 0 ⇒ х = 0; х = -4.
4. Функция непрерывна, асимптот нет.
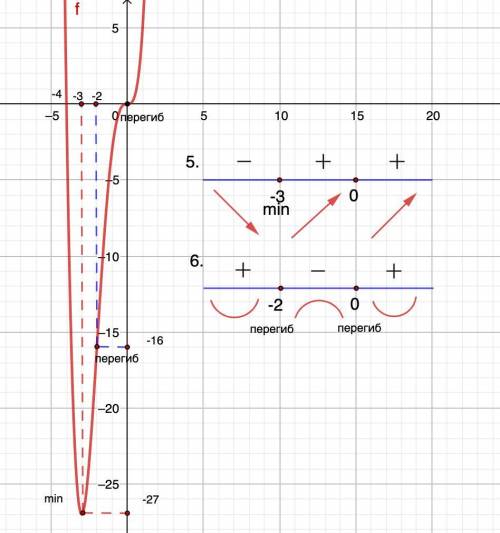
5. Возрастание, убывание, экстремумы.
Найдем производную, приравняем к нулю, найдем корни и отметим их на числовой оси. Определим знак производной на промежутках. Если "+" - функция возрастает, "-" - убывает.
y' = 4x³ + 4·3x² = 4x³ + 12x² = 4x²(x + 3)
y'=0 ⇒ 4x²(x+3) = 0
x = 0; x = -3
См. рис.
Функция убывает при х∈(-∞; -3];
возрастает при х∈[-3; +∞)
В точке х = -3 производная меняет знак с "-" на "+" ⇒
х (min) = -3
y (-3) = 81-108 = -27
6. Выпуклость, вогнутость.
Найдем производную второго порядка, приравняем к нулю, найдем корни и отметим их на числовой оси. Определим знак второй производной на промежутках. Если "+" - функция вогнутая, "-" - выпуклая.
y'' = 4·3x²+12·2x = 12x² +24x =12x(x+2)
y''=0 ⇒ x=0; x=-2
См. рис.
Функция вогнута при х∈(-∞; -2]∪[0; +∞)
выпукла при x∈[-2; 0]
х=-2 и х=0 - точки перегиба.
у(-2)=16-32 = -16; у(0) = 0
Строим график.
2) b*(a-b)
3) y*(y+b)
4) 3*(x+2y+3x^2)
5) x*(6y+1)
6) 4*(2m-3n)
7) c*(c-1)
8) x^4*(4x-7)