В рассматриваемом шестиразрядном числе abcdef, разряд “a” может принимать значения от 1 до 9 (9 значений), разряд “b” может принимать значения от 0 до 0 (1 значение), разряд “c” может принимать значения от 0 до 9 (10 значений), разряд “d” может принимать значения от 0 до 9 (10 значений), разряд “e” может принимать значения от 4 до 4 (1 значение), разряд “а” может принимать значения от 0 до 9 (10 значений).
Посчитаем всевозможное количество значений, которое может принимать число abcdef.
N=9*1*10*10*1*10=9000
Точно также посчитаем всевозможное количество значений, которое может принимать четырехзначное число wxyz, у которого разряд “w” может принимать значения 1 до 9 (9 значений), разряд “x” может принимать значения от 0 до 9 (10 значений), разряд “y” может принимать значения от 0 до 9 (10 значений), разряд “я” может принимать значения от 0 до 9 (10 значений).
M=9*10*10*10=9000
Как видим M=N. Число шестизначных чисел с двумя неизменяемыми разрядами равно числу четырехзначных чисел.


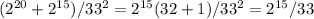
y = k*x+b
k = (By-Ay) / (Bx-Ax)= (5-2)/(3+1) = 3/4 - наклон касательной.
b = By - k*Bx = 5 - 3/4*3 = 2 3/4 = 2.75
Уравнение параболы с вершиной на оси ОУ
Y = a*x² + c
Уравнение касательной к функции
Y = Y'(x)*x + c
Производная параболы
Y'(Bx) = 2*a*Y(Bx)
a = k/2 = 3/8 - размах параболы.
Неизвестное - с - сдвиг параболу по оси ОУ..
Точка В принадлежит и касательной и параболе.
By = 3/8 *Bx + c
5 = 3/8* 3 + c
c = 5 - 9/8 = 3.175
Уравнение параболы
Y = 3/8*x² + 3.175 - ответ
Проверка графиками на рисунке в приложении.