
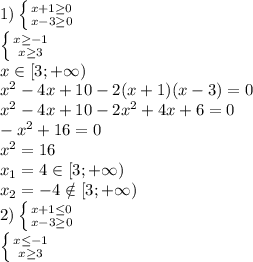
![x \in\emptyset \\3) \left \{ {{x+1 \geq 0} \atop {x-3 \leq 0}} \right. \\ \left \{ {{x \geq -1} \atop {x \leq 3}} \right. \\ x \in [-1;3] \\x^2-4x+10+2(x+1)(x-3)=0 \\x^2-4x+10+2x^2-4x-6=0 \\3x^2-8x^2+4=0 \\D=64-48=16=4^2 \\x_1= \frac{8-4}{6} = \frac{2}{3} \in [-1;3] \\x_2= \frac{8+4}{6} =2\in [-1;3] \\4)\left \{ {{x+1 \leq 0} \atop {x-3 \leq 0}} \right. \\ \left \{ {{x \leq -1} \atop {x \leq 3}} \right. \\x \in (-\infty;-1] \\x^2-4x+10-2(x+1)(x-3)=0 \\x^2-4x+10-2x^2+4x+6=0 \\-x^2+16=0 \\x^2=16](/tpl/images/0817/8619/da656.png)
![x_1=4 \notin (-\infty;-1] \\x_2=-4 \in (-\infty;-1]](/tpl/images/0817/8619/58684.png)
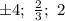
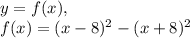
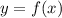 — прямая пропорциональность.
— прямая пропорциональность. — прямая пропорциональность, то есть доказать, что в выражении
— прямая пропорциональность, то есть доказать, что в выражении 
 находится в первой степени (не
находится в первой степени (не 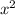 , не
, не 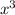 , не
, не 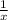 и не
и не 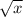 , а просто
, а просто  ).
). . Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид
. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид 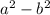 , где
, где 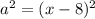 , и
, и 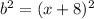 . Формула «разность квадратов» раскрывается так:
. Формула «разность квадратов» раскрывается так: 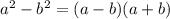 .
.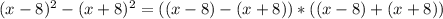
 .
.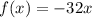 ,
,  находится в первой степени, а значит зависимость
находится в первой степени, а значит зависимость  — есть прямая пропорциональность. Доказано.
— есть прямая пропорциональность. Доказано.
Разбиваем на совокупность уравнений
Решаем каждое из них:
1)
Нули подмодульных выражений:
Значит решения рассматриваем на интервалах:
2)
Аналогично, нули -1 и 3.
ответ: