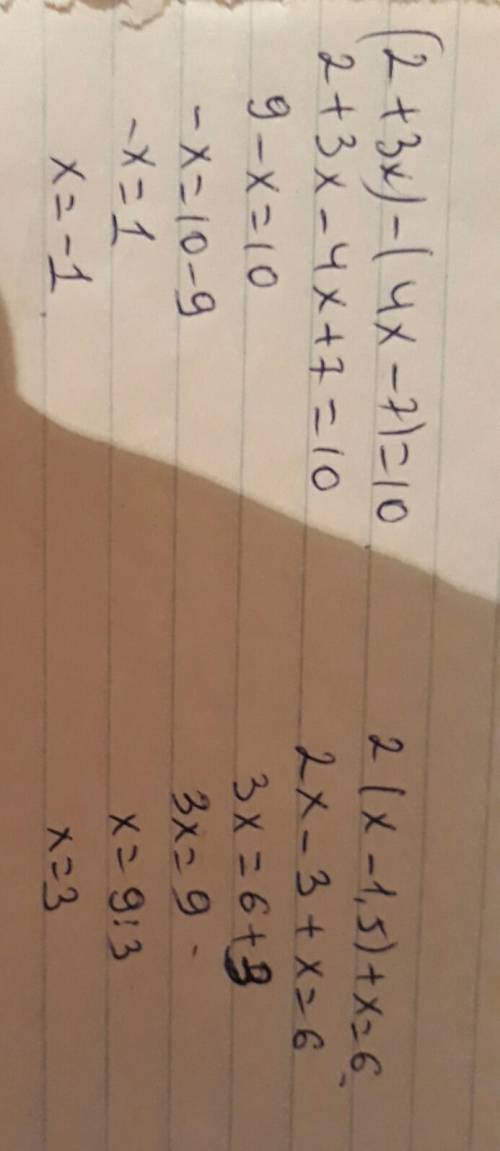
Алгебра: Решить уравнения 3/4=27 (2+-7)=10 2(х-1,5)+х=6

Решить уравнения 3/4=27 (2+-7)=10 2(х-1,5)+х=6

👇

Увидеть ответ

Ответ:

vadim252525

04.12.2022

Первый не решается. ты неправильно написал
Решить уравнения 3/4=27 (2+-7)=10 2(х-1,5)+х=6

4,7(99 оценок)

Ответ:

kirstav64

04.12.2022

2+3х-4х+7=10
4х+3х=10-2-7
7х=1
х=7:1
х=7

4,4(55 оценок)

Открыть все ответы

Ответ:

мадя21

04.12.2022

Давайте разберемся с этим вопросом шаг за шагом.

Начнем с упрощения левой части уравнения. У нас есть такое выражение: c^6 × g^6 : (c^2)^3. Чтобы его упростить, мы должны использовать правила степеней.

Сначала возведем c в шестую степень и получим c^(6+6) = c^12. Затем, развернем (c^2)^3, что даст нам (c^2)^(3*1) = c^6.

Теперь, подставим эти упрощенные значения обратно в исходное уравнение:
c^12 × g^6 : c^6 = 1:64

Для упрощения уравнения дальше, мы можем сократить c^6 с обеих сторон, так как они находятся в числителе и знаменателе.
Таким образом, у нас остается c^6 × g^6 = 1:64.

Теперь, мы можем избавиться от деления в правой части уравнения, умножив обе стороны на 64.
Таким образом, получим c^6 × g^6 × 64 = 1.

Для упрощения уравнения еще больше, мы можем поделить обе стороны на c^6 × 64.
Получим g^6 = 1/(c^6 × 64).

Для того чтобы найти значение g, возведем обе стороны уравнения в шестую степень, чтобы избавиться от степени 6 на g.
Получим g^6^6 = (1/(c^6 × 64))^6.

Теперь, мы можем вычислить правую сторону уравнения. Начнем с 1/(c^6 × 64), чтобы упростить его. Мы можем разложить 64 на 2^6, так что:
1/(c^6 × 64) = 1/(c^6 × 2^6) = 1/(c^6 × 2^6) = 1/((c × 2)^6).

Подставим этот результат обратно в уравнение:
g^6^6 = (1/((c × 2)^6))^6.

Затем, возведем обе стороны в шестую степень:
g^6^6^6 = ((1/((c × 2)^6))^6)^6.

Теперь, мы можем упростить правую сторону уравнения. Когда мы возводим дробь в степень, мы возводим и числитель, и знаменатель в эту степень. Таким образом, для ((1/((c × 2)^6))^6)^6 мы должны возвести числитель и знаменатель в степень 6.
В числителе у нас будет 1^6 = 1, а в знаменателе ((c × 2)^6)^6 = (c × 2)^(6*6) = (c × 2)^36.

Теперь у нас уравнение имеет вид:
g^6^6^6 = 1/((c × 2)^36).

И чтобы найти значение g, мы возводим обе стороны уравнения в 1/36 степень:
(g^6^6^6)^(1/36) = (1/((c × 2)^36))^(1/36).

Теперь мы можем сократить степень и получить значение для g:
g^6 = 1/((c × 2)^1) = 1/(c × 2).

Чтобы избавиться от степени 6, мы возведем обе стороны уравнения в 1/6 степень:
(g^6)^(1/6) = (1/(c × 2))^(1/6).

И наконец, мы получили окончательный ответ для значения g:
g = (1/(c × 2))^(1/6).

Итак, окончательный ответ для значения g, если c^6 × g^6 : (c^2)^3 = 1:64, будет: g = (1/(c × 2))^(1/6).

4,8(95 оценок)

Ответ:

polilol2018

04.12.2022

x^2 - 3x + 2 = (x - 1)(x - 2) < 0

Решением этого неравенства является промежуток (1, 2)

Разложим на множители левую часть второго неравенства:

ax^2 - (3a + 1)x + 3 = (ax^2 - x) - (3ax - 3) = x(ax - 1) - 3(ax - 1) = (x - 3)(ax - 1) = a(x - 3)(x - 1/a)

Возможны 5 вариантов.

1) a > 1/3. Тогда решение неравенства – промежуток (1/a, 3). Нужно, чтобы промежуток (1, 2) полностью содержался в нём, так будет, если 1/a < 1. Объединяем с условием a > 1/3 и получаем часть ответа: a > 1.

2) a = 1/3. У второго неравенства нет решений.

3) 0 < a < 1/3. Решение неравенства – промежуток (3, 1/a); такой промежуток никогда не содержит (1, 2).

4) a = 0. Второе неравенство превращается в 3 - x < 0, x > 3. Не подходит.

5) a < 0. Решение второго неравенства – промежуток (1/a, 3), при этом 1/a < 0. Подходит.

ответ. $(-\infty,0)\cup(1,\infty)$