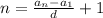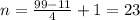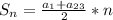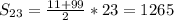
Можно на образовать 192 чисел.
Объяснение:
чтобы числа делились на 2, она должна быть четным.
То есть число должно заканчиваться либо на 2 либо на 8.
Если взять в пример число 23578 мы можем составить ещё 6 чисел заменя цифры (цифры которые мы заменяем это ×) 2×××8. 6×4=24
Но теперь таким же образом мы заменяем первую цифру, а раз у нас остались 4 цифры. Мы делаем: 24×4= 96. И так как в конце у нас может быть либо 2 либо 8. Мы делаем: 96×2=192. Так мы и получили наш ответ.
Я не учитывала десятичные дроби. Надеюсь правельно.