x2=3*2^2-1/4*2^2+1=12-1/16+1=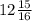
x100=3*100^2-1/4*100^2+1=30000+1-1/40000=30000\frac{39999}{40000}
последовательность является строго монотонной возрастающей, но не имеет предела, так что это доказать невозможно. Строго монотонна она потому что при неограниченном возрастании n первое слагаемое в рекурентной формуле неограниченно возрастает, а второе слагаемое постоянно убывает, в то время как 3е остается неизменным. То есть на каждом новом шаге мы все из большего вычитаем все меньшее. А предела не имеет так как послеовательноть не является ограниченной, это раз, и не выполняется критерий коши для сходимости последовательности, т.е. она не является фундаментальной, это 2
Забыл: Xn+1=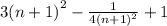
рассмотрим последние цифры чисел во втором она равна 5, а так как сумма двух чисел заканчивается на 8, то у первого она равна 3;
если мы первому приписываем 2, а во втором отбрасываем 5 и получаем равные числа, то во втором числе перед 5 идет 2, а так как в первом перед 2 идет 3, то и во втором перед 2 идет 3;
рассмотрим: если первое число трехзначное и мы приписываем к нему 2 то оно становится 4-ех значным, но второе число максимум 4-ех значное, поэтому отбросив 5 мы не получим 4-ехзначное, а это значит, что второе число двухзначное
запишем его так а3, а второе а325, так как известно что их сумма равна 1338, то а=1; а значит числа 13 и 1325
D=b^2-4ac, приравниваем к нулю, подставляем a и c, решаем уравнение относительно b:
0=b^2-4*1*25 => 0=b^2-100 => b^2=100 => b=+/-10
- ответ: b=+/-10
1) x1 и x2 должны быть в 4 раза больше данного уравнения.
Решим уравнение x^2-6x-1=0
D=6^2-4*(-1)*1=36+4=40 => √D=√40=√4*10=2√10
x1,2=(6+/-2√10)/2
В 4 раза больше, умножаем на 4 => x1,2=(24+/-8√10)/2 => Формула x1,2 = (-b)+/-√b^2-4ac . Считаем: b=-24, D=8√10=√64*10=√640 => (-24)^2=576 => 640-576= 64 => c=-16 => Уравнение: x^2-24x-16=0
- Надеюсь, правильно).