Объяснение:
Чтобы решить эту задачу, нужно знать как минимум 2 операции с матрицами:
Сложение/вычитание матриц. Если у тебя есть матрица A с элементами
(т.е. на i строке j столбца находится число ), и некоторая другая матрица той же размерности B с элементами 
, то в итоговой матрице C = A + B элементы 
, с вычитанием все то же самое, только разность a и b. На практике это выглядит как сумма (или разность) соответствующих чиселУмножение матриц на некоторую константу. Если умножать матрицу A с элементами на некоторое постоянное число C, то C*A =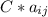 
, т.е. умножаете это число на каждый элемент матрицы.Теперь давайте найдем по условию 3A
![3A = \left[\begin{array}{cc}12&-3\\9&6\end{array}\right]](/tpl/images/0988/6779/046d9.png)
Теперь 2B:
![2B = \left[\begin{array}{cc}-4&2\\10&6\end{array}\right]](/tpl/images/0988/6779/f0fc3.png)
Теперь поэлементно из одного вычитаем другое:
![C = 3A - 2B = \left[\begin{array}{cc}16&-5\\-1&0\end{array}\right]](/tpl/images/0988/6779/e2957.png)
Наверно так?
Пусть время работы рабочего = x ч, тогда время работы ученика x+3. Объём, который каждый должен был выполнить- 40 деталей. Отсюда выражаем производительность ученика и рабочего
производительность рабочего - 40/x
производительность ученика - 40/x+3
Зная, что рабочий выпускал за час на 3 детали больше, составим уравнение:
40/x - 40/x+3 = 3
40/x - 40/x+3 - 3 = 0
Приведя к общему знаменателю получим:
40x+120-40x-3x²-9x/x(x+3) = 0
-3x²-9x+120/x(x+3)
x ≠ 0;x≠-3 поскольку знаменатель дроби не может быть равным нулю.
Решим квадратное уравнение в числителе:
-3x² - 9x + 120 = 0,
x² + 3x - 40 = 0,
D = b² - 4ac = 9 + 160 = 169 > 0, 2 корня
x1 = -3 - 13/2 = -16/2 = -8 - не удовл. усл. задачи.
x2 = -3 + 13/2 = 10/2 = 5
5 ч - работал рабочий, тогда 5+3 = 8 ч - работал ученик. Из этого получаем:
1)40 / 8 = 5(дет/час) - выпускал ученик. Задача решена.
2). Насчёт второго задания. Если я правильно понял, то надо упростить выражение (0.5x^4 * y^-3)^-2 = (0.5)^-2 * (x^4)^-2 * (y^-3)^-2 = 4 * x^-8 * y^6 = 4 * 1/x^8 * y6 = 4y^6/x^8
x-154=0
x=154