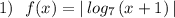
Сначала строим график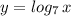 
, затем сдвигаем его на 1 единицу влево вдоль оси ОХ, получаем график функции 
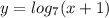. А потом отображаем ту часть графика, которая лежит ниже оси ОХ , в верхнюю полуплоскость и получим график заданной функции 
.
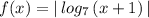Как видно из графика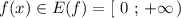 
. См. рис.
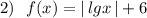
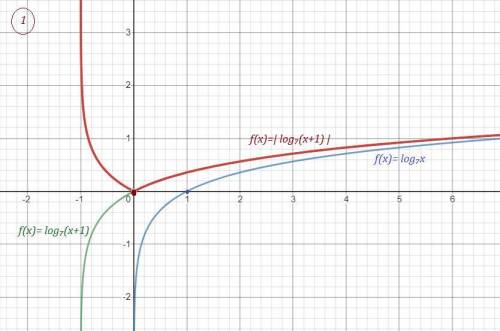
Сначала строим график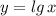 
, затем отображаем ту часть графика, которая лежит ниже оси ОХ , в верхнюю полуплоскость и получим график функции 
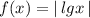. Потом смещаем этот график на 6 единиц вверх вдоль оси ОУ , получим график заданной функции .
Как видно из графика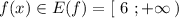 
. См. рис.
Объяснение:
а). D(y)=R
б). E(y)=R
в). Находим первую производную функции:
y' = 2·x-4
Приравниваем ее к нулю:
2·x-4 = 0
x1 = 2
Вычисляем значения функции
у(2) = -1
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
y'' = 2
Вычисляем:
y''(2) = 2>0 - значит точка x = 2 точка минимума функции.
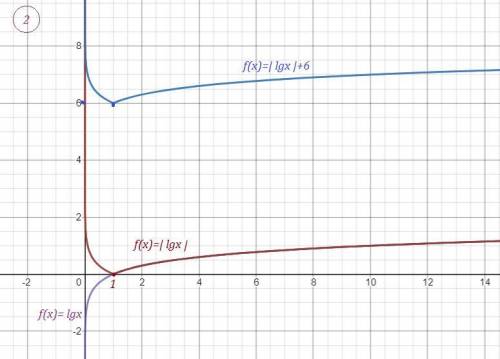
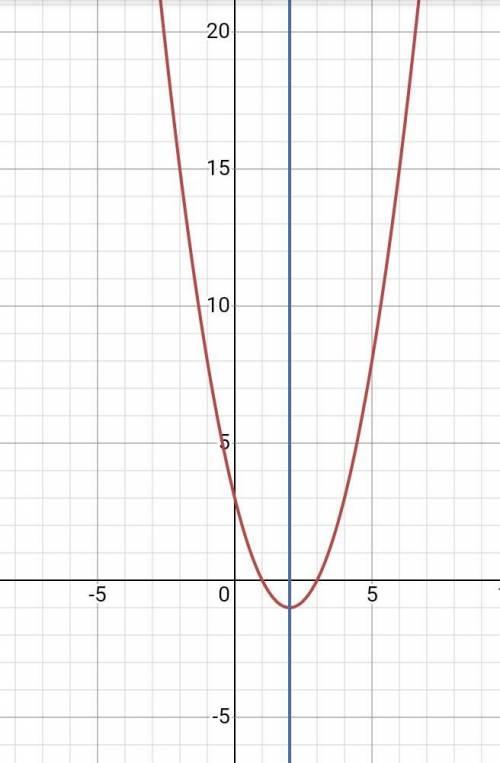
г). Ось симметрии параболы проходит через вершину и перпендикулярно оси Х. Координата х вершины:
х = -b/(2a) = (-4)/2 = -2
Уравнение оси симметрии: х=2 (смотри график)
д). х²-4х+3=0
х1=1, х2=3
А 162 кг получают 8 лошадей и 15 коров, т.е 8х+15у=162.
Решаем систему уравнений:
5х=7у+3
8х+15у=162
х=(7у+3)/5
8(7у+3)/5+15у=162
56у+24+75у=810
131у=786
у=786/131
у=6
х=(7*6+3)/5
х=9
ответ: ежедневно одна лошадь получает 9кг сена, одна корова - 6 кг сена.