Пусть a и b - две смежные стороны прямоугольника, тогда составим cистему уравнений:
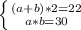
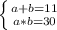
Выразим a через b:
a = 11-b
Подставим во второе уравнение a:
b*(11-b) = 30
b² - 11b + 30 = 0
D = 121 - 120 = 1
b₁ = (11 + 1) / 2 = 6
b₂ = (11 - 1) / 2 = 5
Тогда a₁ = 11 - 6 = 5
a₂ = 11 - 5 = 6
Пусть меньшая сторона — х метров, тогда большая — х+8 метров. Зная площадь площадки, составим и решим мат. модель:
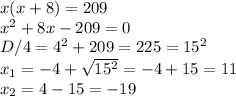
Отрицательный корень отбрасывает, т.к. длина не может быть отрицательной.
Следовательно, меньшая сторона — х = 11 метров;
большая — х+8 = 11+8 = 19 метров.
Для определения кол-ва упаковок материала для бордюра, вычислим периметр площадки:
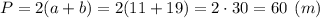
Необходимое количество упаковок равно:
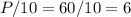
 м.Большая сторона детской площадки равна:
м.Большая сторона детской площадки равна: 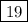 м.Необходимое количество упаковок равно:
м.Необходимое количество упаковок равно:  .
.
ответ: h1=h5=5/3м = 1 2/3 м
h2=h4=8/3м= 2 2/3 м
Объяснение:
Учитывая , что OB - ось симметрии параболы , то в качестве начала координат выберет точку O . Тогда AC лежит на оси x , а OB лежит на оси y. Поскольку вершина лежит на оси y , то парабола имеет вид:
y=a*x^2 +b
Коэффициент b соответствует вершине параболы
b=OB= 3м
Длинны отрезков OA=OC=12/2=6 соответствуют положительному корню параболы :
a* 6^2+3=0
a= -3/36= -1/12
Таким образом парабола имеет вид:
y= 3 - x^2/12
Найдём высоты столбов
Нумерацию столбов будем считать слева направо.
h1=h5=y(+-4м)=3 -16/12 = 3-4/3= 5/3 м
h2=h4=y(+-2м)=3 -4/12= 3-1/3= 8/3 м
а - длина прямоугольника
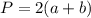 (1)
(1)
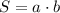 (2)
(2)
b - ширина прямоугольника
=================================================================
Р=22 см
S=30 см²
а - ? см
b - ? см
Решение:
из формулы площади прямоугольника (2) выводим формулу нахождения ширины
подставляем в формулу периметра прямоугольника (1)
умножаем на а для того, чтобы избавиться от знаменателя
подставим в уравнение данные P и S
Квадратное уравнение имеет вид:
Считаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
Следовательно, стороны равны 6см и 5см соответственно
ответ: 6см и 5см стороны прямоугольника.
Проверка:
Р=2(а+b)=2(6+5)=2·11=22 (см)
S=a·b=6·5=30 (м²)