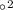 )
) =9+
=9+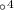
Для начала разложим знаменатель на множители, для этого найдем корни уравнения
x²+6x+5=0
x₁=(-3+4)/2=1/2; x₂=(-3-4)/2=-7/2
Тогда:
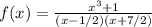
a) при x=-1 знаменатель дроби ≠0, а значит функция непрерывна в этой точке и определена
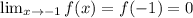 :
:
b) при x=-5 знаменатель дроби также ≠0
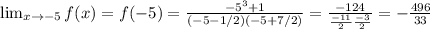
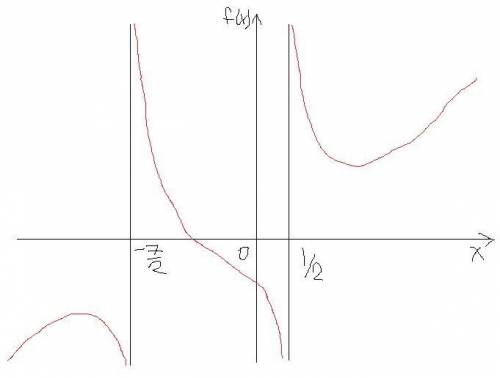
c) Асимптоты (вертикальные) будут при x=x₁, x₂, когда знаменатель=0.
Чертеж - на рисунке.
d) Наклонная асимптота определяется:
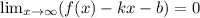
При x→∞ можно оставить в числителе и знаменателе только старшие степени:
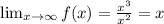
отсюда: k=1, b=0
И наклонная асимптота имеет зависимость: y=x.
Пусть первое число - это Х; а второе число - это У;
По условию задачи Х+У=71; а Х-У=31; - это система уравнений.
Чтобы ее решить надо выразить одну переменную через другую. Например, выразим в первом уравнении У через Х и потом подставим во второе уравнение.
Итак: У=71-Х; Теперь это значение У пишем в нижнее уравнение: Х-(71-Х)=31. Раскроем скобки по правилу (если перед скобками стоит знак минус, то знаки в скобках меняются на противоположные). То есть, Х-71+Х=31;
2Х-71=31;
2Х=31+71;
2Х=102;
Х=51;
У=71-Х. Подставим наше значение Х в эту формулу и вычислим значение У.
Значит так: У=71-х, следовательно У=71-51;
У=20;