х - у = 8
х + у = - 3
Выразим у из каждого уравнения:
у = х - 8
у = - х - 3
Построим графики двух этих функций. Это линейные функции, графиком являются прямые. Для построения каждой прямой надо знать две точки.
у = х – 8
х1 = 0 х2 = 1
у1 = -8 у2 = -7
(0; -8) (1; -7)
у = - х - 3
х1 = 0 х2 = 1
у1 = - 3 у2 = -4
(0; -3) (1; -4)
По данным точкам строим две прямые. Находим точку пересечения. Координаты точки пересечения будут ответом в данной системе.
х = 2,5
у = -5,5
Чертёж прилагается.
ответ: (2,5; -5,5)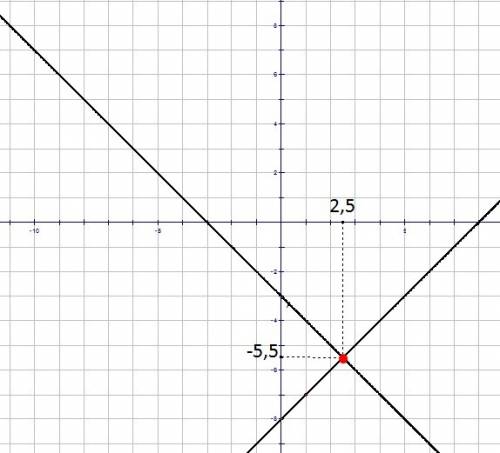
5
2^(x^2-8x+19) > 16
2^(x^2-8x+19) > 2^4
так как основание больше 1 то знак не меняем
x^2-8x+19 > 4
x^2-8x+15 > 0
D = 64 - 60 = 4
x12=(8+-2)/2=5 3
(x-3)(x-5) > 0
метод интервалов
(3) (5)
x ∈(-∞ 3) U (5 + ∞)
7
(x²-8x+16)^(x-6) < 1
((x-4)^2)^(x-6) < (x-4)^0
проверим когда основание равно 0 x=4
степень (х-6)<0 значит х=4 не корень
так как основание слева всегда больше 0 то рассмотрим 2 случае
1. основание >0 и <1
x∈(3 5) тогда
2(x-6)>0
x>6 решений нет
2 основание больше 1
x∈(-∞ 3) U (5 +∞)
2(x-6) < 0
x<6 решение x∈(-∞ 3) U ( 5 6)
Jответ x∈(-∞ 3) U ( 5 6)
560\(х-10) - 560\х = 1
560х-560х+5600-х²+10х=0
х²-10х-5600=0
х=80
ответ: 80 км\час.