ответ: решение во вкладке
Объяснение:
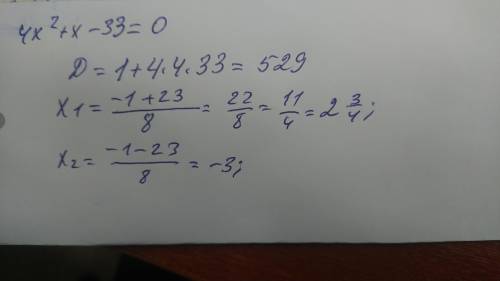
пусть одно число х,второе у..
тогда среднее арифметическое равно (х+у)/2=7 -умножим обе часть на 2,чтобы избавиться от знаменателя
х (в квадрате) -у (в квадрате)=14
тогда получим, что
х+у=14
х (в квадрате) -у (в квадрате)=14
выразим из первого уравнения,х,и подставим во второе,и получим,
х=14-у
(14-у) в квадрате-у в квадрате=14.
раскроем скобки второго уравнения.
196+у (в квадрате)-28у-у(в квадрате)=14
приведём подобные и получим,
-28у=14-196
-28у=-182
у=6,5.
тогда,х=14-6,5=7,5.
и найдём сумму квадратов этих чисел
7,5 в квадрате+6,5 в квадрате=98,5
4x² + x - 33 = 0 D = b²-4ac = 1 + 4·4·33 = 529 = 23²
x₁₂ = (-b±√D)/2a
x₁ = (-1+23):8 = 22/8 = 2,75
x₂ = (-1-23):8 = -24/8 = -3
ответ: {-3; 2,75}
PS. Если у квадратного уравнения есть корни, то левую его часть можно представить в виде произведения по формуле:
ax² + bx + c = a(x - x₁)(x - x₂),
где х - переменная; х₁, х₂ - корни квадратного уравнения