Question

Индукция 2*2+3*5++(n+1)(3n-1)=n(2n^+5n+1)/2 нужно доказать . !

Answer 1

В равенстве слева сумма имеет общий член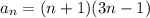 $a_n=(n+1)(3n-1)$

1) Базис индукции: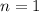 $n=1$

$(1+1)\cdot (3\cdot 1-1)~=4=\dfrac{2\cdot 1^2+5\cdot 1+1}{2}=4$

2) Предположим, что и для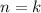 $n=k$ верно равенство

$2\cdot 2+3\cdot 5+...+(k+1)(3k-1)=\dfrac{k(2k^2+5k+1)}{2}$

3) Индукционный переход: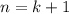 $n=k+1$

$\underbrace{2\cdot 2+3\cdot 5+...+(k+1)(3k-1)}_{\frac{k(2k^2+5k+1)}{2}}+(k+2)(3k+2)=\\ \\ \\ =\dfrac{(k+1)(2(k+1)^2+5(k+1)+1)}{2}\\ \\ \\ \dfrac{k(2k^2+5k+1)}{2}+(k+2)(3k+2)=\dfrac{(k+1)(2k^2+4k+2+5k+5+1)}{2}\\ \\ \\ \dfrac{2k^3+5k^2+k}{2}+3k^2+8k+4=\dfrac{(k+1)(2k^2+9k+8)}{2}\\ \\ \\ \dfrac{2k^3+5k^2+k+6k^2+16k+8}{2}=\dfrac{2k^3+9k^2+8k+2k^2+9k+8}{2}$

$\dfrac{2k^3+11k^2+17k+8}{2}=\dfrac{2k^3+11k^2+17k+8}{2}$

Равенство верно для всех натуральных n. Что и требовалось доказать.