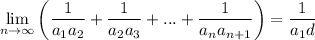Исследуйте на четность функцию :
1) y = f(x) = - 8x + x² + x³
2) y = f(x) = √(x³ + x²) - 31*| x³ |
ни четные ,ни нечетные
Объяснение:
1)
f(x) = - 8x + x² + x³ ; Область Определения Функции: D(f) = R
функция ни чётная ,ни нечётная
проверяем:
Функция является четной, когда f(x)=f(-x) , нечетной, когда f(-x)=-f(x)
а) f(-x) = - 8*(-x) +(- x)² +(- x)³ = 8x + x² - x³ ≠ f(-x)
Как видим, f(x)≠f(-x), значит функция не является четной.
б)
f(-x) ≠ - f(-x) → функция не является нечетной
- - - - - -
2)
y = f(x) = √(x³ + x²) - 31*| x³ | ,
D(f) : x³ + x² ≥ 0 ⇔ x²(x+1) ≥ 0 ⇒ x ≥ -1 * * * x ∈ [ -1 ; ∞) * * *
ООФ не симметрично относительно начало координат
* * * не определен , если x ∈ ( -∞ ; - 1) * * *
функция ни чётная ,ни нечётная
а) 8170
б) ≈ 0,71
Объяснение:
а)
Количество выбора m элементов из n - это число сочетаний из n по m:
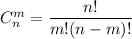
Девочек должно быть не меньше трех. Значит возможны варианты выбора семи школьников в комитет:
3 девочки из семи и 4 мальчика из девяти (применяем правило произведения):
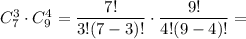
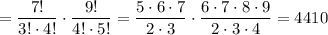
4 девочки и 3 мальчика:
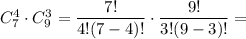
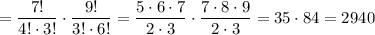
5 девочек и 2 мальчика:
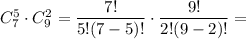
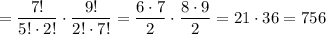
6 девочек и 1 мальчик:
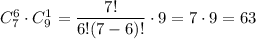
и, наконец, все 7 человек - девочки .
По правилу суммы:
4410 + 2940 + 756 + 63 + 1 = 8170 - количество выбрать 7 человек в комитет так, чтобы в нем было не менее трех девочек.
б)
Всего школьников: 9 + 7 = 16 человек.
Количество выбрать 7 человек из шестнадцати:
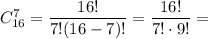
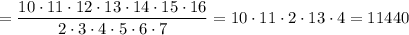
Вероятность того, что в комитете будет не менее трех девочек:
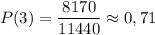
Распишем сначала сумму для удобства и потом подсчитаем предел
Переходя к пределу при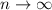 мы получим
мы получим
ответ: