Пусть первое число равно 3а,тогда второе равно а,третье число равно b
Тогда имеет место система:
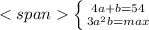
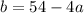
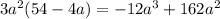
По условию функция вида 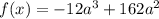
Должна принимать максимальное значение на области определения:
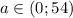
Рассмотрим эту функцию:
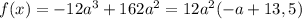
Очевидно,что она принмает положительные значения на интервале:
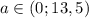
В точке,где функция принимает максимальное значения касательная к функции есть константа вида 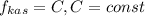
То есть тангенс угла наклона касательной равен нулю:
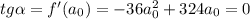
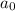 точка касания
точка касания
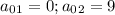
Первая точка не подходит по условию задачи,значит
а=9,3a=27,b=54-4*9=18
Оба этих уравнения являются уравнениями окружности.
Общее уравнение окружности:
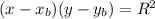
где 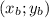 -координаты вершины окружности, R-радиус
-координаты вершины окружности, R-радиус
a) 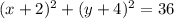
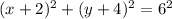
(-2;-4)-вершина, R=6
В системе координат отмечаем точку с координатами (-2;-4) и чертим окружность с центром в этой точке радиусом равным 6. Это и есть график нашей функции.(Совет-выбрать единичный отрезок равный 1 клеточке тетради)
б)[ tex]x^{2}+(y-1)^{2}=2,25[/tex]
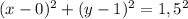
(0;1)-вершина, R=1,5
В системе координат отмечаем точку с координатами (0;1)) и чертим окружность с центром в этой точке радиусом равным 1,5. Это и есть график нашей функции.(Совет-выбрать единичный отрезок равный двум клеточкам тетради)