Question

Mатематический индукция 1*2*3+2*3*4++n(n+1)(n+2)=1/4 n(n+1)(n+2)(n+3) нужно доказать . !

Answer 1

$1\cdot 2\cdot 3+2\cdot 3\cdot 4+...+n(n+1)(n+2)=\dfrac{1}{4}n(n+1)(n+2)(n+3)$

В равенстве слева сумма имеет общий член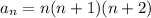 $a_n=n(n+1)(n+2)$

1) Базис индукции: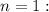 $n =1 :$

$1\cdot (1+1)\cdot (1+2)=\dfrac{1}{4}\cdot 1\cdot (1+1)\cdot (1+2)\cdot (1+3)\\ \\ 6=6$

2) Предположим, что и для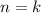 $n=k$ верно равенство

$1\cdot 2\cdot 3+2\cdot 3\cdot 4+...+k(k+1)(k+2)=\dfrac{1}{4}k(k+1)(k+2)(k+3)$

3) Индукционный переход:

$\underbrace{1\cdot 2\cdot 3+2\cdot 3\cdot 4+...+k(k+1)(k+2)}_{\frac{1}{4}k(k+1)(k+2)(k+3)}+(k+1)(k+2)(k+3)=\\ \\ =\dfrac{1}{4}(k+1)(k+2)(k+3)(k+4)\\ \\ \\ \dfrac{1}{4}k(k+1)(k+2)(k+3)+(k+1)(k+2)(k+3)=\dfrac{1}{4}(k+1)(k+2)(k+3)(k+4)\\ \\ \\ \dfrac{1}{4}(k+1)(k+2)(k+3)(k+4)=\dfrac{1}{4}(k+1)(k+2)(k+3)(k+4)$

Равенство выполняется для всех натуральных n. Что и требовалось доказать.