через точку A(2;-1) проходит бесконечное множество прямых, но только одна будет параллельна заданной прямой y-3x =0
запишем в виде y=3x ; угловой коэффициент k=3
прямые будут параллельны , если угловые коээфициенты РАВНЫ
Уравнение прямой, проходящей через данную точку A(x1, y1) в данном направлении, определяемом угловым коэффициентом k и координатами точки А
y - y1 = k(x - x1).
подставим
y - (-1) = 3(x - 2)
y+1 =3x-6
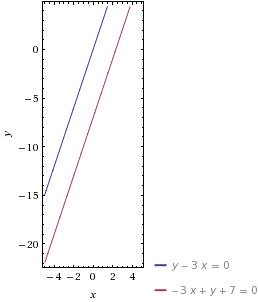
y-3x+7=0 - ЭТО уравнение прямой, параллельной данной прямой и проходящей через данную точку A
смотри рисунок во вложении
Площадь трапеции равна произведению полусуммы оснований на высоту.
На чертеже трапеции опустите высоту из угла В на основание АД - получите прямоугольный треугольник с углом при точке В, образованным стороной АВ и высотой, в 60 градусов и противолежащим высоте углом в 30 градусов.
Высота определится из этого полученного прямоугольного треугольника, как катет прямоугольного треугольника, лежащий против угла в 30 градусов, который равен половине гипотенузы, то есть стороны АВ:
h = AB/2 = 6 (см).
Площадь:
S = h(АД + ВД)/2 = 132 (см2).
13\10х+1\5=7\10х²
Умножаем обе части на 10
13х+2=7х²
Переносим
13х+2-7х²=0
-7х²-13х-2=0
Дискриминант b²-4ac
D=(-13)²-4×7×(-2)=√169+56=√225
x1=-b-√d\2a=2
x2=-b-√d\2a=-1\7
2)Раскрываем скобки и вычисляем
x²-6x+9+x²+8x+16-(x²-10x+25)=17x+24
x²-6x+9+x²+8x+16-x²+10x-25=17x+24
12x+x²+0=17x+24
12x+x²=17x+24
Переносим в лево подобные
12x+x²-17x-24=0
Приводим подобные
-5x²+x²-24=0
x²-5x-24=0
Дискриминант
D=b²-4ac=(-5)²-4×1×(-24)=√121=11
x1=-b-√d\2a=8
x2=-b-√d\2a=-3