1.
Вероятность рассчитывается как отношение благоприятных исходов к общему числу исходов.
Поскольку в мешке А 3 белых шара, а общее число шаров 3+2=5, то вероятность достать белый шар из мешка А:
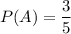
Поскольку в мешке В 3 белых шара, а общее число шаров 3+4=7, то вероятность достать белый шар из мешка В:
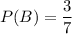
Так как вероятность достать белые шары из мешков А и В независимы, то достать белые шары и из мешка А и из мешка В равна произведению двух ранее найденных вероятностей:
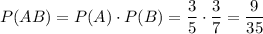
2.
Поскольку в мешке В 4 белых шара, а общее число шаров 3+4=7, то вероятность достать черный шар из мешка В:
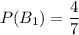
Предположим, что после первой попытки из мешка В достали черный шар. Тогда, черных шаров в нем осталось 3, а общее число шаров в нем стало 6. Вероятность достать следующий черный шар:

Поскольку второе событие осуществимо только при условии наступления первого, то вероятность достать два черных шара подряд равна произведению двух вероятностей:
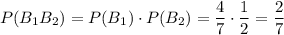
Даны координаты вершин пирамиды:
A(4, 4, -10) ; B(4, 10, 2) ; C(2, 8, 4) ; D(9, 6, 4).
1) уравнение плоскости АВС и ее нормальный вектор
Находим векторы АВ и АС.
АВ = (0;6; 12), АС = (-2; 4; 14).
Их векторное произведение равно.
i j k | i j
0 6 12 | 0 6
-2 4 14 | -2 4 = 84i - 21j +0k - 0j - 4+ 12k = 36i - 24j + 12k.
Нормальный вектор к плоскости АВС равен (36; -24; 12).
Его же можно выразить, разделив на кратную величину 12:
(3; -2; 1).
Уравнение плоскости АВС найдём по точке А и нормальному вектору : A(x − x0) + B(y − y0) + C(z − z0) = 0
Если теперь в уравнении раскрыть скобки и привести подобные члены, получим общее уравнение плоскости:
Ax + By + Cz + D = 0 ,
где D = −Ax0 − By0 − Cz0, A = 3, B = -2, C = 1, точка A(4, 4, -10).
Найдём значение D:
D = -3*4 - (-2)*4 - 1*(-10) = -12 + 8 + 10 = 6.
Уравнение АВС: 3x - 2y + z + 6 = 0.
2) отрезки, которые отрезает плоскость АВС от осей координат.
Для этого уравнение плоскости АВС представить в "отрезках".
Уравнение АВС: 3x - 2y + z + 6 = 0.
3x - 2y + z = -6. Разделим обе части уравнения на -6:
(3/-6)x - (2/-6)y + (1/-6)z = 1.
Получаем: (-1/2)x + (1/3)y + (-1/6)z = 1.
Это и есть длины отрезков, отсекаемые плоскостью АВС на осях:
Ох: (-1/2), Оу: (1/3), Oz: ((-1/6).
3) уравнение плоскости pi, которое проходит через вершину D параллельно к грани ABC.
Общее уравнение заданной плоскости имеет вид:
Ax+By+Cz+D=0 (2)
Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (2) плоскости, проходящей через точку M0(x0, y0, z0) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (2). Далее нужно найти такое значение D, при котором точка M0(x0, y0, z0) удовлетворяла уравнению плоскости (2):
Ax0+By0+Cz0+D=0. (3)
Решим (3) относительно D:
D=−(Ax0+By0+Cz0) (4)
Координаты нормального вектора определены:
A = 3, B = −2, C = 1.
Подставляя координаты точки D и координаты нормального вектора в (4), получим:
D=−(Ax0 + By0 + Cz0) = −(3*9 + (−2)*6 +1*4) = −19.
Подставляя значения A, B, C, D в (2), получим уравнение плоскости, проходящей через точку D(9, 6, 4) и параллельной плоскости ABC:
3 x − 2 y + z − 19 = 0.
48-8%
х=48*100/8
х=600
Следовательно в школе всего 600 учеников