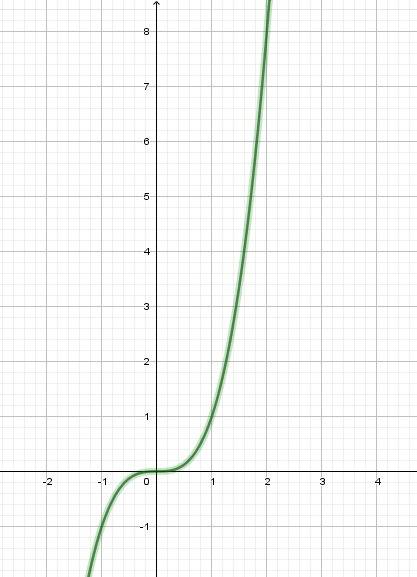
Точки построения графика: (0;0), (±1; ±1), (±2; ±8). График является нечетной.
Подставим координаты точки A(-5;125) в график уравнения, получим
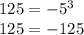
Поскольку равенство не верно, то график функции y = x³ не проходит через точку A(-5;125), т.е. точка не принадлежит графику y = x³
Подставим теперь координаты точки B(4;64), получим
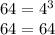
Поскольку равенство тождественно выполняется, то точка B принадлежит графику функции y = x³.
Подставим координаты точки C(-3;-27), имеем
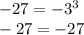
Раз равенство тождественно выполняется, то точка C(-3;-27) принадлежит графику функции y = x³
1) OA = OC = OB = a
Треугольники ОАВ, ОАС и ОВС - прямоугольные с равными катетами, значит они равны по двум катетам. Значит, равны и их гипотенузы:
АВ = АС = ВС.
Треугольник АВС равносторонний, значит его углы равны по 60°.
2) OA = OB = 6 см, OC=8см
ΔОАС = ΔОВС по двум катетам. По теореме Пифагора в ΔОАС:
АС = √(ОА² + ОС²) = √(36 + 64) = √100 = 10 см
ВС = АС = 10 см
ΔОАВ равнобедренный прямоугольный. По теореме Пифагора
АВ = √(ОА² + ОВ²) = √(36 + 36) = 6√2 см
ΔАВС равнобедренный. По теореме косинусов найдем угол АСВ:
cosACB = (CA² + CB² - AB²)/(2·CA·CB) = (100 + 100 - 72)/(2·10·10) =
= 128/200 = 0,64
∠ACB ≈ 50°
∠CAB = ∠CBA ≈ (180° - 50°)/2 ≈ 65°
2) (4x-1)^2=(4х)²-2*4х*1+1²=16х²-8х+1;
3) (2x+3y)^2=(2х)²+2*2х*3у+(3у)²=4х²+12ху+9у²;
4) (x^2-8x)^2=(х²)²-2х²*8х+(8х)²=х^4-16х³+64х²;
5)x^2+4x+4=(х+2)²;
6)25x^2-10xy+y^2=(5х-у)²;
7) (5x+2)^2-20x=25х²+20х+4-20х=25х²+4;
8) 27x^2-3(3x-1)^2=3(9х²-(3х-1)²)=3(3х-(3х-1))*(3х+(3х-1))=3(3х-3х+1)*(3х+3х-1)=3*1(6х-1)=3(6х-1).