![\sqrt{18} - \sqrt{7} = \sqrt{3 {}^{2} \times 2} - \sqrt{7} = \sqrt{ {3}^{2} } - \sqrt{7} = \sqrt[3]{2} - \sqrt{7}](/tpl/images/0837/2390/0d8fe.png)
Объяснение:
1я бригада 300 дет/час
2я бригада 300 -х дет/час
3я бригада 300 +4х дет/час
время выполнения работы
t=((1/4)/(300+300-x)) + ((3/4)/(300+300-x+300+4x))=
=(1/4)[900+3x+3(600-x)]/((600-x)(900+3x))=
=(2700/4)[1/(-3x²+900x+540000)]
t будет иметь минимальное значение при максимальном значении выражения -3x²+900x+540000
по свойству квадратичной функции так как коэффициент при х² меньше 0 то ветки параболы направлены вниз и максимум квадратичной функции будет в вершине
х=-b/2a=900/6=150 деталей в час
Первый решения (короткий).
Замечаем, что по условию нам дано одно и то же время (и там, и там 4 часа). Первым действием узнаем, сколько выкачает один насос за 4 часа.
1) 
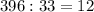м³ выкачивает один насос за 4 часа.
Вторым действием умножим количество воды, которое выкачивает один насос за это время, на 23 (общее кол-во насосов), чтобы узнать, сколько они выкачают за 4 часа.
2) 
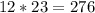м³ воды выкачают 23 насоса за 4 часа.
ответ: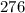 
м³.
Второй решения (более длинный).
Первым действием узнаем общую скорость 33х насосов.
1) 
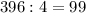м³ выкачивают 33 насоса, работая вместе, в час.
Зная, что это скорость 33 штук, можно найти скорость одного насоса.
2) 
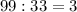м³ выкачивает один насос в час.
Нам нужно узнать, сколько воды выкачают 23 насоса за 4 часа. Третьим действием выясним, сколько воды выкачает один насос за 4 часа.
3) 
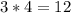м³ воды выкачает один насос за 4 часа.
Остается узнать, сколько воды выкачают 23 штуки за 4 часа.
4) 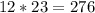м³ воды выкачают 23 насоса за 4 часа.
ответ: 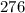м³.
