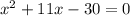
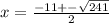
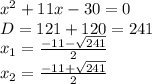
1)2(3x+7)-8(x+3)<_3
6x"+14 - 8x -24 -3 <_0
-2x<_13
x>_ - 6,5 отмечаем на координатной прямой ,точка будет выколотой и [ -6,5. +бесконечность)
2)-3x^2 +8x + 3=0
D = 64- 4*(-3)*3= 64+ 36=100=10^2
x1= -8 +10 / -6 = -2/6=-1/3
x2=-8 - 10 /-6 = 3
OTVET : -1/3 ; 3
3)4x^2 - 4x - 15 <0
D= 16-4*4*(-15) = 16+ 240= 256= 16^2
x1= 4+16 / 8= 20/8=5/4
x2=4-16/ 8= -12/16 = -3/4
4)8+2x-6 = 4x+7
-2x = 5
x=-2,5
5) 5x +4 _> 2
3-2x <_ 4
5x _> -2
-2x<_1
x_>-2/5
x>_-1/2
Если ветви параболы направлены вниз, то квадратичная функция у=ах²+bx+c в вершине параболы принимает наибольшее значение и коэффициент при х² меньше 0, то есть а<0.
Координаты вершины х(верш)= -b/2a
y(верш)=ах²(верш)+bx(верш)+с=a(-b/2a)²+b(-b/2a)+c
x(верш)=-(а-3)/2а
а(а-3)² (а-3)² (а-3)² (а-3)²
у(верш)= - +1=4 , - - 3=0 ,
4а² 2а 4а 2а
а²-6а+9-2(а²-6а+9)-12а
=0
4а
-а²+6а-9-12а=0
-а²-6а-9=0 , а²+6а+9=0 , (а+3)²=0 , а=-3