Функция убывает при x ∈ [- 2; 0] ; [2; + ∞).
Функция возрастает при x ∈ (- ∞; - 2] ; [0; 2].
Объяснение:
y = - x⁴ + 8x² - 16
y' = - 4x³ + 16x
y' = 0
- 4x³ + 16x = 0
4x(x² - 4) = 0
x = 0, x² - 4 = 0
(x - 2)(x + 2) = 0
x = 2 x = - 2
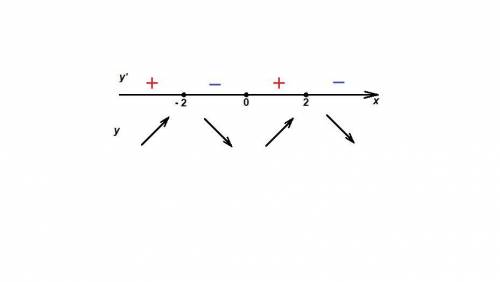
Отметим точки на координатной прямой и определим знаки производной на получившихся интервалах (знаки чередуются, справа минус), см. рисунок.
Если на промежутке производная положительна, то функция возрастает, если отрицательна - убывает.
Функция убывает при x ∈ [- 2; 0] ; [2; + ∞).
Функция возрастает при x ∈ (- ∞; - 2] ; [0; 2].
a) Найдите значение дроби (2a+b) /(3a+4b) ,если известно ,что b/a-3
(2a+b) / (3a+4b) = (2+b/a) / (3+4*b/a) =(2+3) /(3+4*3) = 5/15 = 1/3 .
б) Преобразуйте выражение
( 5/(a²+10a+25) ) : ( (a²+10a) /(a² -25) -(a+5)/(a-5) ) и найдите его числовое величина при a = -2 .
( 5/(a²+10a+25) ) : ( (a²+10a) /(a² -25) - (a+5)/(a-5) ) =
( 5/(a²+10a+25) ) : ( (a²+10a) /(a -5)(a+5) - (a+5)/(a-5) )
( 5/(a+5)²) : ( (a²+10a -(a+5)² ) / (a -5)(a+5) )=
( 5/(a+5)²) : ( ( a²+10a -a²-10a -25 ) / (a -5)(a+5) ) =
(5/(a+5)² ) : ( (-25 ) / (a -5)(a+5) ) =
( 5/(a+5)² ) * ( (5- a)(a+5) / 25 ) = (5 -a) / 5(a+5) [ a = -2] =
= ( 5 -(-2) ) /5( -2+5) = 7 / 15.
Объяснение:
Координкты x во 2 степени имеет такие координаты-
(0;0)
(1;1)
(2;4)
Так же само с противоположной стороны.