Мы имеем ограничения — корни и знаменатель. Проблема в том, что для числителя правой части сложно написать адекватное ОДЗ. А можно ли обойтись без него?
Оказывается, можно. Достаточно записать, что:
![\left \{ {{7-x\geq 0} \atop {x-10}} \right. \Rightarrow x\in(1;7]](/tpl/images/0450/0668/e88fe.png)
Возведём в квадрат обе части (так как они положительны, имеем право сделать это) и посмотрим, что получится:
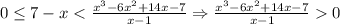
Дробь положительна, если и числитель, и знаменатель имеют одинаковый знак. По ограничению, которое мы записали выше, знаменатель положителен, значит, числитель обязан быть положительным, то есть это страшное ОДЗ выполняется автоматически. Теперь можно решить получившееся неравенство:

Пересекая полученное решение с ограничениями, получим правильный ответ.
ответ: ![(1;2)\cup(3;7]](/tpl/images/0450/0668/a5885.png)
1) 2х - 3(1 + х) = 5 + х 2) 2(3 - х) + 7х = 4 - (3х + 2)
2х - 3 - 3х = 5 + х 6 - 2х + 7х = 4 - 3х - 2
2х - 3х - х = 5 + 3 - 2х + 7х + 3х = 4 - 2 - 6
- 2х = 8 8х = - 4
х = 8 : (-2) х = - 4 : 8
х = - 4 х = - 0,5
Задача. Пусть х - задуманное число:
3х - 10 = 0,5х
3х - 0,5х = 10
2,5х = 10
х = 10 : 2,5
х = 4
Проверка: 4 * 3 - 10 = 0,5 * 4
12 - 10 = 2 - полученное число вдвое меньше задуманного
ответ: Лена задумала число 4.
2=k/-4
k=-8
Подставляем k и 2 точку:
8=-8/-1
8=8 > проходит