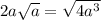
х ∈ (-0,5; +∞)
Объяснение:
|2x+5|-1<6x-2
1) 2x+5 ≥ 0 (2x ≥ 5 или х ≥ 2,5 ) ⇒ |2x+5| = 2x+5
|2x+5|-1<6x-2 ⇒ 2x+5 -1<6x-2
2х + 4 < 6x - 2
4 + 2 < 6x - 2x
6 < 4x
6/4 < x
1,5 < x или х > 1,5 (ОДЗ: х≥ 2,5) ⇒ решение данной части: х ∈ [2,5; +∞)
2) 2x+5 < 0 (2x < 5 или х < 2,5 ) ⇒ |2x+5| = -(2x+5)
|2x+5|-1<6x-2 ⇒ -(2x+5) -1<6x-2
-2x-5 -1<6x-2
-2х -6 < 6x - 2
-6 + 2 < 6x + 2x
-4 < 8x
-4/8 < x
-0,5 < x или х > -0,5 (ОДЗ: х < 2,5) ⇒ решение данной части: x ∈ (-0,5;2,5)
объединяя решение первой части (х ∈ [2,5; +∞)) и второй (x ∈ (-0,5;2,5)) получаем общее решение х ∈ (-0,5; +∞)
Объяснение:
Когда в ёмкость налили 4 литра 30-процентного водного раствора некоторого вещества, а затем добавили 12 литров 40-процентного раствора того же вещества, то
1) сухого вещества в нем станет:4*0,3+12*0,4=1,24,8= 6 л
2) весь объём будет: 4+12=16 л
3) концентрация раствора будет: 6/16
Нам нужен 25% ный раствор
Пусть надо добавить х литров воды, тогда концентрация станет: 6/(16+х) и она должна равняться 0,25
6/(16+х) =0,25 ( умножим обе части уравнения на 4)
24/(16+х) =1⇒16+х=24⇒х=24-16⇒х=8
ответ: 8 литров