Р = a + b + c - периметр треугольника
a : b = 3 : 4 - отношение катетов
с = 50 см - гипотенуза
По теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Пусть х - коэффициент пропорциональности, тогда а = 3х см - один катет, 4х см - второй катет. Уравнение:
(3х)² + (4х)² = 50²
9х² + 16х² = 2500
25х² = 2500
х² = 2500 : 25
х² = 100
х = √100
х = ±10 (отрицательное значение не рассматриваем)
3х = 3 · 10 = 30 (см) - катет а
4х = 4 · 10 = 40 (см) - катет b
Р = 30 + 40 + 50 = 120 см - периметр этого прямоугольника
ответ: 120 см.
Объяснение:
Вероятнее всего, требуется доказать следующее тождество /
Найімовірніше, потрібно довести наступне тотожність:
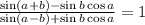
Решение / Рішення
Рассмотрим и преобразуем левую часть /
Розглянемо і перетворимо ліву частину:
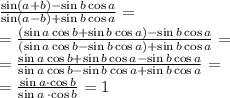
При преобразовании левой части мы получили 1, т.е. то же, что содержится в правой части. Следовательно, тождество верно. Что и требовалось доказать.
/
При перетворенні лівої частини ми отримали 1, тобто те ж, що міститься в правій частині.
Отже, тотожність вірно.
Що і потрібно довести
При решении использовалась формула синуса суммы и синуса разности двух углов:
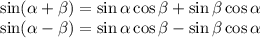
2) четыре — если три прямые пересекаются в одной точке;
3) одна — если все 4 прямые пересекаются в одной точке.