1) (х-1)(х+7)
1) (х-1)(х+7)х*х+7х-х-7
1) (х-1)(х+7)х*х+7х-х-7х²+7х-х-7
1) (х-1)(х+7)х*х+7х-х-7х²+7х-х-7х²+6х-7
1) (х-1)(х+7)х*х+7х-х-7х²+7х-х-7х²+6х-72) (6х+4)(2-3х)
1) (х-1)(х+7)х*х+7х-х-7х²+7х-х-7х²+6х-72) (6х+4)(2-3х)6х*2-6х*3х+4*2-4*3х
1) (х-1)(х+7)х*х+7х-х-7х²+7х-х-7х²+6х-72) (6х+4)(2-3х)6х*2-6х*3х+4*2-4*3х12х-18х²+8-12х
1) (х-1)(х+7)х*х+7х-х-7х²+7х-х-7х²+6х-72) (6х+4)(2-3х)6х*2-6х*3х+4*2-4*3х12х-18х²+8-12х-18х²+8
1) (х-1)(х+7)х*х+7х-х-7х²+7х-х-7х²+6х-72) (6х+4)(2-3х)6х*2-6х*3х+4*2-4*3х12х-18х²+8-12х-18х²+83) (х²-2х)(2х+4+х²)
1) (х-1)(х+7)х*х+7х-х-7х²+7х-х-7х²+6х-72) (6х+4)(2-3х)6х*2-6х*3х+4*2-4*3х12х-18х²+8-12х-18х²+83) (х²-2х)(2х+4+х²)х²(2х+4+х²)-2х(2х+4+х²)
1) (х-1)(х+7)х*х+7х-х-7х²+7х-х-7х²+6х-72) (6х+4)(2-3х)6х*2-6х*3х+4*2-4*3х12х-18х²+8-12х-18х²+83) (х²-2х)(2х+4+х²)х²(2х+4+х²)-2х(2х+4+х²)2х³+4х²+х⁴-4х²-8х-2х³
1) (х-1)(х+7)х*х+7х-х-7х²+7х-х-7х²+6х-72) (6х+4)(2-3х)6х*2-6х*3х+4*2-4*3х12х-18х²+8-12х-18х²+83) (х²-2х)(2х+4+х²)х²(2х+4+х²)-2х(2х+4+х²)2х³+4х²+х⁴-4х²-8х-2х³х⁴-8х
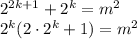
Пусть сначала k>0.
Так как первый сомножитель делится на 2, а второй не делится, то 2^k должно быть полным квадратом, т.е. k четно; k=2K. Если первый сомножитель представляется полным квадратом, то и второй сомножитель - полный квадрат.
2^(2K+1)+1=m^2
2^(2K+1)=(m-1)(m+1)
Стало быть, m нечетно; m=2M+1
2^(2K+1)=2M*2(M+1)
2^(2K-1)=M*(M+1)
Последнее равенство при целых M, K выполняется, если:
- 2K-1=0 - не может такого быть
- M=0, тогда 2K-1=0, чего опять быть не может.
Итак, единственный возможный вариант - k=0. Подставим:
2^1+2^0=m^2
m^2=3
Это уравнение не имеет целочисленных корней.
Теперь k<0.
k=-1: 2^(-1)+2^(-1)=m^2
1=m^2
m=+-1
k<-2: первое число - несократимая дробь со знаменателем -(2k+1), второе - дробь со знаменателем (-k). При рассматриваемых k -(2k+1)>-k, так что сумма дробей не является целым числом.
ответ. (k,m)=(-1,+-1).
(√5-√10) (√5+√10) = √5²-√10² = 5 - 10 = - 5