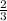от того, что осталось после первого деня, то после второго дня работы осталась 
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
Объем V = a^2*h = 4
h = 4/a^2
Боковые грани все одинаковые, прямоугольники axh. Их периметр
P = 2(a + h) - должен быть минимальным. Подставляем h из равенства
P = 2(a + 4/a^2) = 2(a^3 + 4)/a^2
Минимум функции будет в точке, где производная равна 0.
P ' = 2*(3a^2*a^2 - 2a*(a^3 + 4))/a^4 = 2*(3a^3 - 2a^3 - 8)/a^3 = 0
a^3 - 8 = 0
a^3 = 8
a = 2 - сторона квадрата в основании параллелепипеда
h = 4/a^2 = 4/4 = 1 - высота параллелепипеда
P = 2(a + h) = 2(2 + 1) = 2*3 = 6