Объяснение:
Чтобы упростить выражение 2a(а + b - с) - 2b(а - b - с) + 2c(а - b + с) откроем скобки и приведем подобные слагаемые.
Откроем скобки в заданном выражении
Для того, чтобы открыть скобки нам нужно вспомним несколько правил:
распределительный закон умножения относительно сложения и вычитания;
правило открытия скобок перед которыми стоит знак плюс;
правило открытия скобок перед которыми стоит знак минус.
Распределительный закон умножения относительно сложения звучит так: Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Аналогично распределительный закон звучит и для вычитания.
Правило раскрытия скобок, перед которыми стоит знак минус: скобки вместе со знаком минус опускаются, а знаки всех слагаемых в скобках заменяются на противоположные.
Правило раскрытия скобок, перед которыми стоит знак плюс или не стоит никакого знака, таково: скобки вместе с этим знаком опускаются, а знаки всех слагаемых в скобках сохраняются.
2а(а + b - с) - 2b(а - b - с) + 2с(а - b + с) = 2a * a + 2a * b - 2a * c - (2b * a - 2b * b - 2b * c) + 2c * a - 2c * b + 2c * c = 2a^2 + 2ab - 2ac - 2ab + 2b^2 + 2bc + 2ac - 2bc + 2c^2.
Сгруппируем и приведем подобные слагаемые
Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
2a^2 + 2ab - 2ac - 2ab + 2b^2 + 2bc + 2ac - 2bc + 2c^2 = 2a^2 + 2b^2 + 2c^2.
ответ: 2a^2 + 2b^2 + 2c^2.
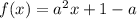 и
и 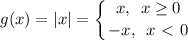
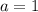 , то
, то 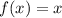 и
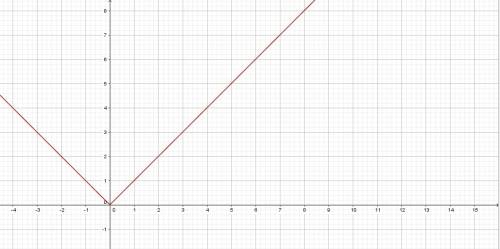
и 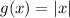 . График функции f(x) совпадает с графиком функции g(x) при x≥0
. График функции f(x) совпадает с графиком функции g(x) при x≥0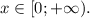
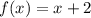 - прямая, которая проходит через точки (0;2) и (-2;0). График функции f(x) = x+2 параллельный графику функции f(x)=|x| при x≥0, f(x) с g(x) пересекаются в одной точке
- прямая, которая проходит через точки (0;2) и (-2;0). График функции f(x) = x+2 параллельный графику функции f(x)=|x| при x≥0, f(x) с g(x) пересекаются в одной точке ![a \in (-\infty;-1]\cup[1;+\infty)](/tpl/images/0775/7169/67fd3.png) уравнение имеет одно решение.
уравнение имеет одно решение.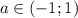 уравнение имеет 2 решения.
уравнение имеет 2 решения.