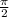 = 1
= 1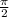 = 0
= 0 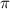 n. 2
n. 2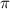 означает, что будет сделан полный оборот, и точка вернётся в тоже место, в котором была.Например выражение
означает, что будет сделан полный оборот, и точка вернётся в тоже место, в котором была.Например выражение 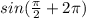 говорит нам о том, что перед тем, как искать значение
говорит нам о том, что перед тем, как искать значение  нужно "пройти" по окружности(в нашем случае против часовой стрелки, т.к. +,а не -)2
нужно "пройти" по окружности(в нашем случае против часовой стрелки, т.к. +,а не -)2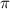 .
.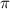 =3.14 радиан и = 180 градусам. т.е. если у нас есть +- 2
=3.14 радиан и = 180 градусам. т.е. если у нас есть +- 2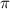 , это значит, что мы делаем ровно один круг по окружности(360 градусов).Фактически, если у тебя есть такое выражение:
, это значит, что мы делаем ровно один круг по окружности(360 градусов).Фактически, если у тебя есть такое выражение: , то ты можешь смело отбрасывать 2
, то ты можешь смело отбрасывать 2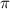 , т.к. они,фактически, не влияют на решение. Другое же дело, если у тебя стоит просто
, т.к. они,фактически, не влияют на решение. Другое же дело, если у тебя стоит просто 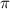 . Тогда тебе придётся перенести точку на 180 градусов, и уже к ней прибавлять угол(Пример:
. Тогда тебе придётся перенести точку на 180 градусов, и уже к ней прибавлять угол(Пример: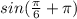 . Здесь тебе придётся перенести точку на 180 градусов и прибавить к ней угол sin
. Здесь тебе придётся перенести точку на 180 градусов и прибавить к ней угол sin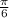 .Это будет третья четверть, а значит знак в ответе будет отрицательный(ответ:
.Это будет третья четверть, а значит знак в ответе будет отрицательный(ответ: .). Число оборотов, это n.При чём оно может быть не целым, отрицательным и т.д. но это уже совсем другая история.А вообще, наглядно это усваивается гораздо проще.Поэтому рекомендую подойти к учителю и лично попросить объяснить.
.). Число оборотов, это n.При чём оно может быть не целым, отрицательным и т.д. но это уже совсем другая история.А вообще, наглядно это усваивается гораздо проще.Поэтому рекомендую подойти к учителю и лично попросить объяснить.
Объяснение:В том случае, если катер будет двигаться против течения реки, его скорость будет равна разнице собственной скорости и скорости течения реки.
Получим:
х - 1,9 км/ч.
Если катер будет двигаться по течению реки, его скорость будет равна сумме собственной скорости и скорости течения реки.
Получим:
х + 1,9 км/ч.
Если подставить вместо значения х любое натуральное число, получим:
х = 10 км/ч.
х - 1,9 = 8,1 км/ч (скорость катера против течения реки).
10 + 1,9 = 11,9 км/ч (скорость катера по течению реки).
х - 1,9 км/ч.
1) ОДЗ: cos(x) <> 0 => x <> p/2 + 2pn
Домножим обе части равенства на cos(x) <> 0:
2с^2 - 2sc + s - c = 0
(c - s)(2c - 1) = 0
cos(x) = sin(x) => 1 - tg(x) = 0 => tg(x) = 1 => x = p/4 + pn
2c - 1 = 0
cos(x) = 0.5 => x = +-p/3 + 2pn
В итоге x = +-p/3 + 2pn, x = p/4 + pn.
Так как нас интересуют значения х на промежутке
[3p/2;3p], т.е 1.5р...3р, то подходят 2p - p/3, 2p + p/4, 2p + p/3.
ответ: 2p + p/3, 2p - p/3, 2p + p/4.
2) sinx+1/1-cos2x=sinx+1/1+cos(p/2+x)
(s+1)/(2*s*s) = (s + 1)/(1 - s)
ОДЗ:
sin(x) <> 0 => x <> pn
sin(x) <> 1 => x <> p/2 + 2pn
s + 1 = 0 => sin(x) = -1 => x = 2pn - p/2
2s*s = 1 - s
2s*s + s - 1 = 0
Решим как квадратное уравнение:
s1 = 2/4 = 0.5 => sin(x) = 0.5 => x = (-1)^n*(p/6) + pn
s2 = -4/4 = -1 (такие корни уже были)
В итоге: x = 2pn - p/2, x = (-1)^n*(p/6) + pn.
Причем x <> pn, x <> p/2 + 2pn.
По условию нужно выбрать корни на промежутке [-3p/2;-p/2], т. е. от -1.5р до -0.5р.
2pn - p/2:
при n = 1: x = -1.5p, но так как x <> p/2 + 2pn, этот корень не подходит.
при n = 0: x = -0.5p.
(-1)^n*(p/6) + pn:
при n = -1: x = -p - p/6.
ответ: x = -0.5p, x = -p - p/6.