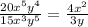
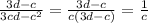

Объяснение:
![\[\begin{gathered}\frac{{20{x^5}{y^4}}}{{15{x^3}{y^5}}}=\frac{{20}}{{15}}{x^{5-3}}{y^{4-5}}=\frac{4}{3}{x^2}{y^{-1}}=\boxed{\frac{{4{x^2}}}{{3y}}} \hfill \\\frac{{3d-c}}{{3cd-{c^2}}}=\frac{{3d-c}}{{c(3d-c)}}=\boxed{\frac{1}{c}} \hfill \\\frac{{3m-3n}}{{{m^2}-{n^2}}}=\frac{{3(m-n)}}{{(m-n)(m+n)}}=\boxed{\frac{3}{{m+n}}} \hfill \\ \end{gathered} \]](/tpl/images/1010/4503/a0d57.png)
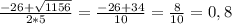

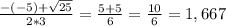

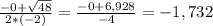
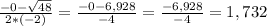
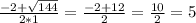
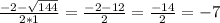
10-4(2x+5)=6y-13
4y-63=5(4x-2y)+2
4y-63=5(4x-2y)+2
4y-63-20x+10y-2=0
14y-65-20x=0
x=0.7y-3.25
10-4(2x+5)=6y-13
3-8x-6y=0
3-8*(0.7y-3.25)-6y=0
3-5.6y+26-6y=0
29-11.6y=0
y=29/11.6
y=2.пятых
14y-65-20x=0
14*2.5-65-20x=0
-30-20x=0
x=-30/20
x=-1.5