Для решения нужно написать уравнение прямой. Известно, что прямая задается уравнением у=а*х+b. Подставляя наши координаты (3;4) и (-6;-2) в уравнение прямой, получаем систему уравнений, из которой находим коэфициент а и b.
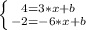 . Решение относительно а дает результат 2/3, т.е. а=2/3, подставив в первое уравнение значение а, имеем b=2. Следовательно уравнение прямой у=(2/3)*х+2. Для вичисления точок пересечения с осями поочередно подставляем 0 вместо у (прямая пересекает ось ОХ), и вместо х (пресекает ось ОУ). (2/3)*х+2=0; х=-3.
. Решение относительно а дает результат 2/3, т.е. а=2/3, подставив в первое уравнение значение а, имеем b=2. Следовательно уравнение прямой у=(2/3)*х+2. Для вичисления точок пересечения с осями поочередно подставляем 0 вместо у (прямая пересекает ось ОХ), и вместо х (пресекает ось ОУ). (2/3)*х+2=0; х=-3.
(2/3)*0+2=у; у=2.
Т.е., точки пересечения с осями координат (-3;0) и (0;2).
x=2
Объяснение:
Асимптота графика - такая прямая, к которой график стремится в определенной области, но никогда не пересекает. Следовательно, функция не может принимать такие значения. А какие значения не может принимать данная функция?
Функция дробно-рациональная( в знаменателе есть переменная). А мы знаем, что знаменатель дроби не должен равняться нулю, значит х не равно двум. А значит прямая вида х=2, это на графике такая прямая, которая параллельна оси Оу, и прохдит через точку 2 - является вертикальной асимптотой графика
Разделим 2-ое уравнение на 1-ое :
Так как в условии задано ограничение на знаменатель прогрессии,
q>0, то q=1/5 .