
Для построение этого вида функций, которые под знаком модуля содержат всю функцию, можно построить отдельно функцию, которая находится под знаком модуля, а затем отобразить относительно оси Ох ту ее часть, для которой значения у – отрицательные. Это позволит получить положительные значения у для всей функции.
Итак, построим параболу, которая будет графиком заданной функции без знака модуля:
у1 = 6x – 5 – x^2.
Сначала найдем ее вершину с формулы х = –b / (2a):
х = –6 / (2*(–1)) = 3
Вычислим значение функции:
у1(3) = 6*3 – 5 – 3^2 = 4.
Получили в точке (3; 4).
Точки пересечения с осью Ох найдем, подставив в уравнение для у1 значение у1 = 0 и решив полученное уравнение:
6x – 5 – x^2 = 0
По теореме Виета или любым другим доступным находим, что корнями уравнения будут значения 1 и 5. Значит функция пересечет ось Ох в точках (1; 0) и (5; 0).
Построенный график – это график функции у1 = 6x – 5 – x^2.
Теперь отображаем относительно оси Ох все, что находится под ней, и получаем график функции у = |6x – 5 – x^2|.
Построить график можно и другим подставляя значения х в заданную функцию с модулем. Но проведенный анализ Вам понять сущность модуля при построении графиков.
Объяснение:
Я к примеру объяснил.
99) Правило: ![\boxed{\ \sqrt{a^2}=|a|\ \ \ ,\ \ \ \sqrt[2n]{a^{2n}}=|a|\ }](/tpl/images/4529/9104/a373f.png) .
.
При извлечении квадратного корня или корня чётной степени ( 2n - обозначение чётного числа ) из а² (или  ) надо не забыть поставить модуль, ведь сам корень чётной степени может быть только неотрицательным . А модуль любого выражения тоже неотрицателен . Причём, если выражение под модулем неотрицательно, то модуль равен самому этому выражению. Если выражение под модулем отрицательно, то модуль равен этому выражению, взятому с противоположным знаком.
) надо не забыть поставить модуль, ведь сам корень чётной степени может быть только неотрицательным . А модуль любого выражения тоже неотрицателен . Причём, если выражение под модулем неотрицательно, то модуль равен самому этому выражению. Если выражение под модулем отрицательно, то модуль равен этому выражению, взятому с противоположным знаком.
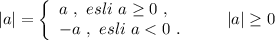
Например, 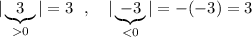 . Как видим, в любом
. Как видим, в любом
случае получаем модуль, равный неотрицательному числу .
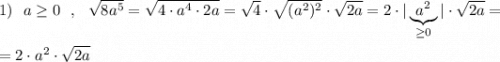
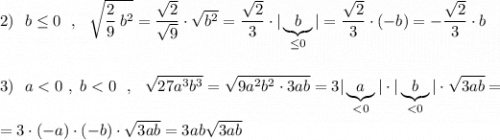
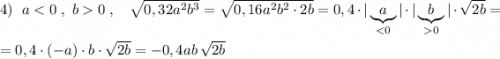
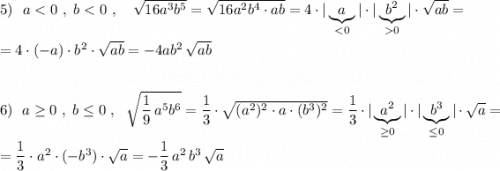
P.S. Обратите внимание, что в 5 примере b<0 , но под модулем записан b² , который несмотря на отрицательное b всё равно будет положительным, и тогда 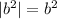 .
.
В 6 примере, так как b≤0 , нечётная степень b тоже будет неположительной, тогда если 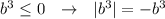 .
.
100) Если 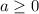 , то
, то ![a=\sqrt{a^2}\ \ ,\ \ a=\sqrt[2n]{a^{2n}}](/tpl/images/4529/9104/decbc.png) .
.
Если 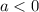 , то
, то ![a=-\sqrt{a^2}\ \ ,\ \ a=-\sqrt[2n]{a^{2n}}](/tpl/images/4529/9104/b5eb6.png) .
.
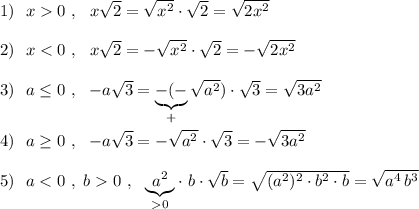

Заметь, что все выражения под знаком квадратного корня или корня чётной степени неотрицательны ! И когда мы внесли под корень множители, получившиеся выражения должны быть неотрицательными .
Например, в 6 примере:
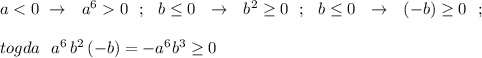
11(1+2y)-9y=37
11+22y-9y=37
13y=37-11
13y=26
y=2
x=1+2*2=1+4=5
ответ: (5;2)
B) выражаем y из 2 уравнения
y=3x-2
подставляем в 1 уравнение
16x-4(3x-2)=5
16x-12x+8=5
4x=5-8
4x=-3
x=-3/4=-0,75
y=3*(-0,75)-2=-2,25-2=-4,25
ответ: (-0,75;-4,25)