1. Доказать тождество
sinα +sin5α+sin7α +sin11α = 4cos2α*cos3α*sin6α
sinα +sin5α+sin7α +sin11α =(sin5α +sinα) +(sin11α+sin7α) =
2sin3α*cos2α +2sin9α*cos2α =2cos2α*(sin9α+sin3α)=
2cos2α*2sin6α*cos3α =4cos2α*cos3α*sin6α
- - - - - - -
2.Найдите значение выражения sin2α*cos5α -sinα*cos6α ,если sinα = -1/√3
- - -
Cначала упростим выражение:
sin2α*cos5α -sinα*cos6α =2sinα*cos∝*cos5α - sinα*cos6α =
sinα(2cos5α*cos∝ - sinα*cos6α )=sinα*(cos6∝+cos4α -cos6α ) =
sinα*cos4α =sinα*(1 - 2sin²2α) = sinα*( 1 -2*(2sinα*cosα)² )=
= sinα*( 1 -8sin²α*cos²α ) =sinα*( 1 -8sin²α*(1 -sin²α) ) = || sinα =-1/√3 ||
= (-1/√3)*( 1 -8*(-1/√3)² *(1 - (-1/√3)² ) = - 1/√3 *( 1- (8/3)*(2/3) ) = 7√3 / 27
5 и 9
Объяснение:
Корни уравнения: 9; -5; 5; -6
(-9 не подходит, так как под корнем будет отрицательное число!)
У нас должно выполниться двойное неравенство:
log₂3≤x≤3π, где x - наш корень
наибольший из корней: 9
сравним его с 3π:
так как 3π≈3*3.14=9.42, то
9<3π - значит и все другие корни меньше чем 3π.
Но при этом каждый из корней должен быть больше log₂3
универсальный)
сравниваем числа:
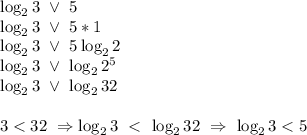
Аналогично проверяем 9
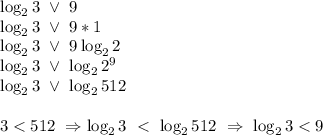
Проверяем оставшиеся числа и выясняем, что подходят только 5 и 9
для данного примера)
так как log₂2=1 и log₂4=2, значит 1<log₂3<2.
Получается, что только числа 5 и 9 будут больше чем log₂3