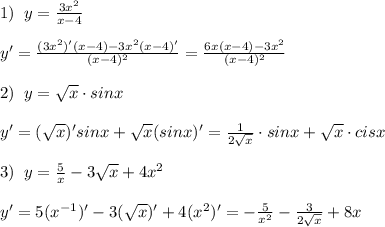
Объяснение:
Задание 1
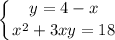
Значение у из первого уравнения подставим во второе уравнение
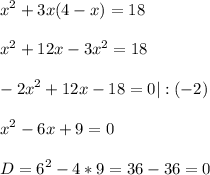
Если дискриминант равен нулю , то квадратное уравнение имеет только один действительный корень, также можно сказать , что квадратное уравнение имеет два действительных корня , которые равны между собой.
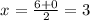

Задание 2
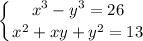
первое уравнение в системе это разность кубов, разложи на множители:
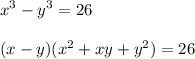
из второго уравнения подставим значение выражения х²+ху+у²
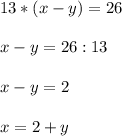
подставим значение х во второе уравнение системы :
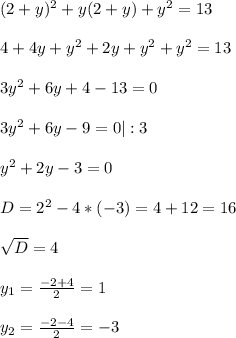
тогда
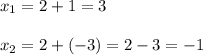
Корни уравнения ( 3 ;1) и ( -1 ; -3)