Объяснение:
1)5х+3х=14+0
8х=14
Х=14 : 8
Х=1,75
2)2у+у=2+4
3у=6
У=6 : 3
У=2
3)первое уравнение домножаем на 2, получается :
8х-10у=12
2х+10у=21
(У сокращаются), остаётся:
8х+2х=12+21
10х=33
Х=3,3
Ищем у:
2х+10у=21
Подставляем найденное значение х
2×3,3+10у=21
6,6+10у=21
10у=21-6,6
10у=14,4
У=14,4 : 10
У=1,44
4) 2х-у=3
х-2,5у=10
Домножаем второй уравнение на ( -2)
2х-у=3
- 2х-5у= -20
Иксы сокращаются , остаётся
6у= -17
У= - 17 : 6
У= - 2,83
Ищем х :
Подставляем найденное значение у в первое уравнение:
2х-(-2,83)=3
2х+2,83=3
2х= 3-2,83
2х=0,17
Х=0,085
5)-
6)-
Объяснение:
из всех правил сдвига графика функций, я выберу те, которые касаются нашей функции
1. если ФУНКЦИЯ умножается на число 0<m<1 , то происходит сжатие её графика вдоль оси oy в 1/m раз
2. если АРГУМЕНТ функции умножается на 0<k<1, то график функции растягивается от оси оу в 1/k раз
3. если к АРГУМЕНТУ функции добавляется константа b y(x+b), то происходит сдвиг (параллельный перенос) графика вдоль оси оx на b единиц влево .
теперь проделаем все это с нашей функцией
начнем с простого
1. у нас ФУНКЦИЯ умножается на число 0< 1/4 <1, значит мы будем сжимать функцию y = cos(x) в 4 раза вдоль оси оу
2. у нас АРГУМЕНТ функции умножается на 0< 1/2 <1, значит мы будем растягивать график у = cos(x) от оси оу в 2 раза
3. а вот теперь тут будет не так просто. поскольку правило 3 справедливо для графика функции y(x+b), нам надо привести свою заданную функцию к такому виду
таким образом у нас будет сдвиг (параллельный перенос) графика
у = cos(x) вдоль оси оx на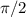 
единиц влево
ну и вот что должно получиться.
Y = 9*x² + 6x + 1
ИССЛЕДОВАНИЕ
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет
2. Пересечение с осью Х. Решаем квадратное уравнение: Y=0
при х1,2 = - 1/3.
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = +∞ - горизонтальных асимптот - нет.
5. Исследование на чётность.Y(-x) = 9*x² - 6*x+1 ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 18*x -6 = 0.
Корень Х= -1/3.
7. Локальные экстремумы. Минимум – Ymin(- 1/3) =0.
8. Интервалы возрастания и убывания. Возрастает - Х∈(-1/3;+∞),
убывает = Х∈(-∞;-1/3)
8. Вторая производная - Y"(x) = 18.
Корня производной - точка перегиба - нет.
9. Вогнутая – «ложка» Х∈(-∞;+∞).
10. Область значений Е(у) У∈(0;+∞)
11. Наклонная асимптота -. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(∞)(9x+6+1)= ∞ - наклонных асимптот - нет
12. График в приложении.