846875
Объяснение:
Всего 6-значных чисел 900000: на первое место можно поставить одну из 9 цифр, на оставшиеся - любую из 10.
Посчитаем, у скольких чисел произведение цифр не делится на 4. Такое бывает в двух случаях:
Произведение цифр нечётное, тогда все цифры нечётные, на каждое место можно независимо выбирать один из 5 вариантов цифры. Таких чисел
Произведение цифр делится на 2, но не на 4, тогда в числе одна из цифр 2 или 6, а остальные - нечетные. Выбрать место для четной цифры можно а после этого расставить цифры - 
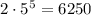Всего получаем 
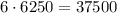чисел.Общее количество чисел, произведение цифр которых не делится на 4, равно 
, значит, искомое количество равно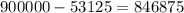 
1. Выбывшие игроки не играли между собой, тогда без учета их игр остальные игроки сыграли 78 партий (при этом все сыграли со всеми
2. Одну игру выбывшие игроки сыграли между собой, тогда эта игра не влияет на кол-во игр других игроков, то есть остальные игроки между собой сыграли 79 игр
Решим задачу наоборот, нам известно, что игроков было n. Надо узнать, сколько сыграно партий. Первый игрок сыграл всего n-1 партмй (поскольку сам с собой он не мог играть), второго мы уже посчитаем как n-2, поскольку одну партию с первым игроком мы уже посчитали. И так далее, пока не дойдет до единицы, а там останется ещё один игрок, все партии которого мы уже посчитали. То есть мы складываем все числа от нуля до n-1.
Поступим так же.
0+1+2+3+4+5+6+7+8+9+10+11+12=78
n-1=12 значит игроков было 13
И еще прибавим двух выьывших игроков
ответ: 15 игроков