1. x^2-4x+40≤0
D = b^2−4ac = 16-160 = -144
D < 0 ⇒ нет корней
Т.к. a = 1 > 0, то x^2−4x+40 > 0 для любых x, следовательно, неравенство x^2-4x+40 ≤ 0 не имеет смысла.
ответ: x∈∅, решений нет.
2. x^2-4x+40<0
Аналогично, как для п 1.
Т.к. a = 1 > 0, то x^2−4x+40 > 0 для любых x, следовательно, неравенство x^2-4x+40 < 0 не имеет смысла.
ответ: x∈∅, решений нет.
3. x^2-4x+4>0
D = 16-16 = 0
D = 16-16 = 0 ⇒ 1 корень
x = -b/2 = 4/2 = 2
Вычислим знаки на каждом интервале:
x<2 | x>2
+ | +
Неравенство строгое, значит точка с абсциссой x=2 — выколотая.
ответ: x∈(−∞; 2)∪(2; +∞) или x<2; x>2.
4. x^2-4x+4≥0
x = 2 (см п. 3.)
Вычислим знаки на каждом интервале:
x<2 | x>2
+ | +
Неравенство нестрогое, значит точка с абсциссой x=2 — входит в решение.
ответ: x∈(−∞; +∞) или x — любое число, x∈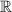 .
.
Объяснение:
2^(2x+1) + 25^(0,5+x) >= 7*10^x
1) (2^2x)*(2^1) + (25^0,5)*(25^x) - 7*10^x >= 0;
2) 2*2^2x + 5*5^2x - 7*2^x*5^x >= 0;
3) Заменим 2^x на t и 5^x на m, тогда 2*t^2 + 5*m^2 - 7*t*m >= 0;
4) Разделим каждый член неравенства на 5*m^2;
5) 2t^2/5m^2 - 7t/5m + 1 >= 0;
6) Разложить на множители
(t/m - 1)*(t/m - 5/2) >= 0;
7) На числовой прямой отмечаем точки 1 и 5/2, определяет знаки на промежутках. Получаем t/m принадлежит (-∞;1]и[5/2;+∞)
8) Обратная замена: (2/5)^x
9) (2/5)^x принадлежит
(-∞;1]и[5/2;+∞), следовательно
x принадлежит (-∞;0]и[-1;+∞)
3x² + 6x - 5x - 10 - x² + 5x + 2 ≤ 0
2x² + 6x - 8 ≤ 0
x² + 3x - 4 ≤ 0
Найдём корни квадратного трёхчлена
D = 9 - 4 * (- 4) = 9 + 16 = 25
Решим неравенство методом интервалов
(x - 1)(x + 4) ≤ 0
+ - +
_______________________________
- 4 1
x ∈ [- 4 , 1]
Целые решения неравенства : - 4 ,- 3 ,- 2 ,- 1 ,0 ,1