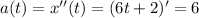
Объяснение:
1.
а) х/7 = 14
х = 98;
б) 8х +11,2 = 0
8х = -11,2
х = -1,4
в) 5х - 1,7 = 3х + 5,3
5х - 3х = 5,3 + 1,7
2х = 7
х = 3,5
г) 3х - (5х - 7) = 21
3х - 5х + 7 = 21
5х - 3 х = 7 - 21
2х = -14
х = -7
2.
х - прочтено страниц во 2-й день
х/3 - прочтено страниц в 1-й день
х + х/3 = 4х/3 - прочтено страниц за 2 дня
4х/3 = 256
х/3 = 64
х = 64 · 3
х = 192
ответ: 3а 2-й день было прочтено 192 страницы
3.
8х - (2х + 5) = 3(2х - 3)
8х - 2х - 5 = 6х - 9
6х - 5 = 6х - 9
-5 ≠ -9
Решений нет
4.
х - было книг во 2-м шкафу
4х - было книг в 1-м шкафу
4х - 24 - стало книг в 1-м шкафу
х + 18 - стало книг во 2-м шкафу
4х - 24 = х + 18
3х = 42
х = 14 - было книг во 2-м шкафу
4х = 56 - было книг в 1-м шкафу
НЕТ НЕ ВЕРНО
|a + b| ≤ |a| + |b| это ВЕРНО
Существует 4 варианта знаков + и - для чисел a и b
1 вариант
Если a > 0 и b > 0
их модули совпадают с их значениями: |a| = a, |b| = b
Из этого следует, что |a + b| = |a| + |b|
2 вариант
Если a < 0 и b > 0
выражение |a + b| можно записать как |b – a|
А выражение |a| + |b| равно сумме абсолютных значений a и b, что больше, чем |b – a|
3 вариант (похож на 2 вариант)
Если a > 0 и b < 0 |a + b|
выражение |a + b| принимает вид |a – b|
А выражение |a| + |b| равно сумме абсолютных значений a и b что также больше чем |a - b|
Поэтому |a + b| < |a| + |b|
4 вариант
Если a < 0 и b < 0
тогда |a + b| = |–a – b| = |-(a + b)|
Но в варианте 1 доказано, что |a + b| = |a| + |b|, следовательно и |–a – b| = |a| + |b|
значит |a + b| ≤ |a| + |b| в зависимости от знаков a и b
а вот |ab| = |a|*|b|
v(t ) = x'(t) = (3t² + 2t + 1)' = 6t+2
a(t) = v'(t) = (6t + 2)' = 6